Giải mục 2 trang 58, 59, 60, 61, 62 SGK Toán 12 tập 1 - Cánh diều

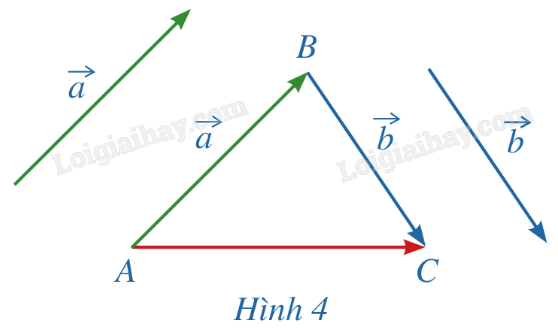
HĐ2

Trả lời câu hỏi Hoạt động 2 trang 58 SGK Toán 12 Cánh diều

Trong không gian, cho 2 vecto \(\vec a\) và \(\vec b\). Lấy một điểm A tùy ý.

a) Vẽ \(\overrightarrow {AB}  = \vec a\), \(\overrightarrow {BC}= \vec b\).

b) Tổng của 2 vecto \(\vec a\) và \(\vec b\) bằng vec tơ nào trong Hình 4?

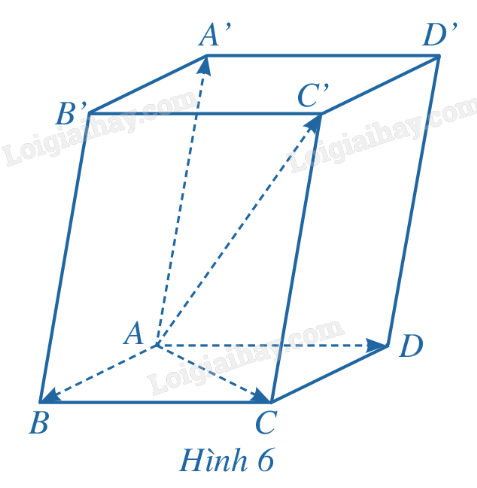
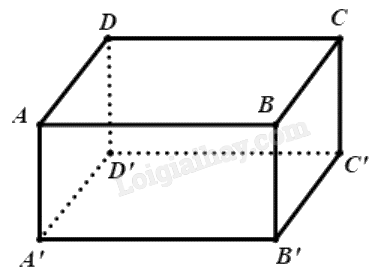
Phương pháp giải:

a) Ghi rõ các bước để vẽ hình.

b) Áp dụng quy tắc 3 điểm \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \).

Lời giải chi tiết:

a)

– Qua A vẽ một đường thẳng song song với \(\vec a\). Trên đường thẳng đó lấy điểm B sao cho \(AB = \left| {\vec a} \right|\) và \(\overrightarrow {AB}\) cùng hướng với \({\vec a}\).

– Qua B vẽ một đường thẳng song song với \(\vec b\). Trên đường thẳng đó lấy điểm C sao cho \(BC = \left| {\vec b} \right|\) và \(\overrightarrow {BC}\) cùng hướng với \({\vec b}\).

b) Ta có: \(\vec a + \vec b = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \).

LT2

Trả lời câu hỏi Luyện tập 2 trang 58 SGK Toán 12 Cánh diều

Cho tứ diện ABCD. Chứng minh rằng \(\overrightarrow {AC}  + \overrightarrow {DB}  = \overrightarrow {AB}  + \overrightarrow {DC} \).

Phương pháp giải:

Áp dụng quy tắc ba điểm.

Lời giải chi tiết:

Theo quy tắc ba điểm, ta có: \(\overrightarrow {AC}  = \overrightarrow {AB}  + \overrightarrow {BC} \); \(\overrightarrow {DB}  = \overrightarrow {DC}  + \overrightarrow {CB} \).

Do đó \(\overrightarrow {AC}  + \overrightarrow {DB}  = \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {DC}  + \overrightarrow {CB} \)

\( = \overrightarrow {AB}  + \overrightarrow {DC}  + \overrightarrow {BC}  + \overrightarrow {CB}  = \overrightarrow {AB}  + \overrightarrow {DC}  + \overrightarrow {BC}  - \overrightarrow {BC}  = \overrightarrow {AB}  + \overrightarrow {DC} \) (đpcm).

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 59 SGK Toán 12 Cánh diều

Cho hình hộp ABCD.A’B’C’D’. Tìm liên hệ giữa \(\overrightarrow {AB}  + \overrightarrow {AD} \) và \(\overrightarrow {AC}\); \(\overrightarrow {AC}  + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \).

Phương pháp giải:

Áp dụng quy tắc hình bình hành.

Lời giải chi tiết:

Xét hình bình hành ABCD:

\(\overrightarrow {AB}  + \overrightarrow {AD} = \overrightarrow {AC} \) (1)

Xét hình bình hành ACCA':

\(\overrightarrow {AC}  + \overrightarrow {AA'}  = \overrightarrow {AC'} \) (2)

Từ (1) và (2) suy ra \(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'}  = \overrightarrow {AC'} \).

LT3

Trả lời câu hỏi Luyện tập 3 trang 59 SGK Toán 12 Cánh diều

Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng: \(\overrightarrow {B'B}  + \overrightarrow {AD}  + \overrightarrow {CD}  = \overrightarrow {B'D} \).

Phương pháp giải:

Áp dụng quy tắc hình hộp.

Lời giải chi tiết:

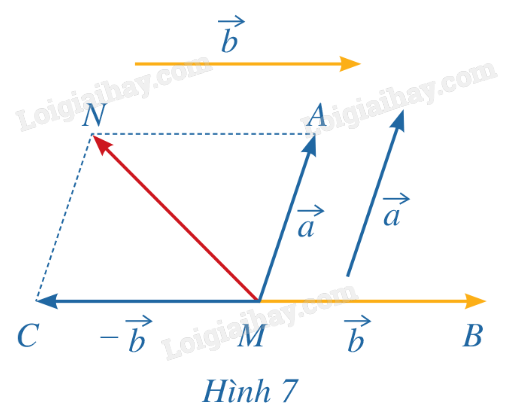
Ta có: \(\overrightarrow {AD}  = \overrightarrow {B'C'} \); \(\overrightarrow {CD}  = \overrightarrow {B'A'} \) (các vecto cùng hướng và cùng độ dài).

Suy ra \(\overrightarrow {B'B}  + \overrightarrow {AD}  + \overrightarrow {CD}  = \overrightarrow {B'B}  + \overrightarrow {B'C'}  + \overrightarrow {B'A'}  = \overrightarrow {B'D} \) (theo quy tắc hình hộp).

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 59 SGK Toán 12 Cánh diều

Trong không gian, cho hai vecto \(\vec a\), \(\vec b\). Lấy một điểm M tùy ý.

a) Vẽ \(\overrightarrow {MA}  = \vec a\), \(\overrightarrow {MB}  = \vec b\), \(\overrightarrow {MC}  = \overrightarrow { - b} \).

b) Tổng của hai vecto \(\vec a\) và \(\overrightarrow { - b} \) bằng vecto nào trong Hình 7.

Phương pháp giải:

Sử dụng quy tắc hình bình hành.

Lời giải chi tiết:

\( \vec{a}\) + (\( - \vec{b}) =\) \(\overrightarrow {MA}  + \overrightarrow {MC}  = \overrightarrow {MN} \) (quy tắc hình bình hành).

LT4

Trả lời câu hỏi Luyện tập 4 trang 59 SGK Toán 12 Cánh diều

Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng: \(\overrightarrow {BB'}  - \overrightarrow {C'B'}  - \overrightarrow {D'C'}  = \overrightarrow {BD'} \).

Phương pháp giải:

Áp dụng quy tắc hình hộp.

Lời giải chi tiết:

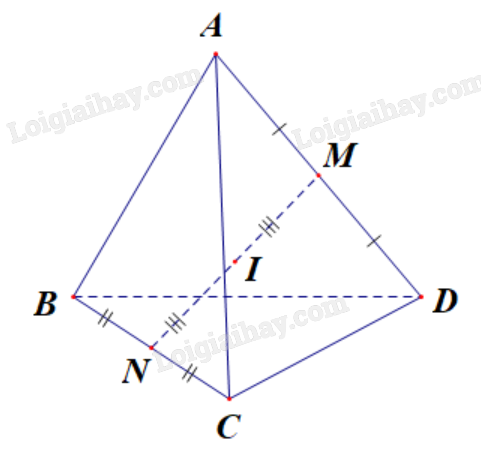
\(\overrightarrow {BB'}  - \overrightarrow {C'B'}  - \overrightarrow {D'C'}  = \overrightarrow {BB'}  + \overrightarrow {B'C'}  + \overrightarrow {C'D'} \)

\( = \overrightarrow {BB'}  + \overrightarrow {BC}  + \overrightarrow {BA}  = \overrightarrow {BD'} \) (theo quy tắc hình hộp).

HĐ5

Trả lời câu hỏi Hoạt động 5 trang 60 SGK Toán 12 Cánh diều

Nêu định nghĩa tích của một số thực \(k \ne 0\) với vecto \(\vec a \ne \vec 0\) trong mặt phẳng.

Lời giải chi tiết:

Cho số thực \(k \ne 0\) và \(vecto\;\vec a \ne \vec 0\). Tích của số k với vecto \(\vec a\) là một vecto, kí hiệu là \(k\vec a\) được xác định như sau:

- Cùng hướng với vecto \(\vec a\) nếu k > 0, ngược hướng với vecto \(\vec a\) nếu k < 0.

- Có độ dài bằng \(\left| k \right|.\left| {\vec a} \right|\).

LT5

Trả lời câu hỏi Luyện tập 5 trang 60 SGK Toán 12 Cánh diều

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điển của các cạnh AD và BC, I là trung điểm của MN. Chứng minh rằng:

a) \(\overrightarrow {MN}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {DC} } \right)\).

b) \(\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  + \overrightarrow {ID}  = \overrightarrow 0 \).

Phương pháp giải:

Sử dụng tính chất ba điểm, khái niệm các vecto bằng nhau, vecto đối nhau.

Lời giải chi tiết:

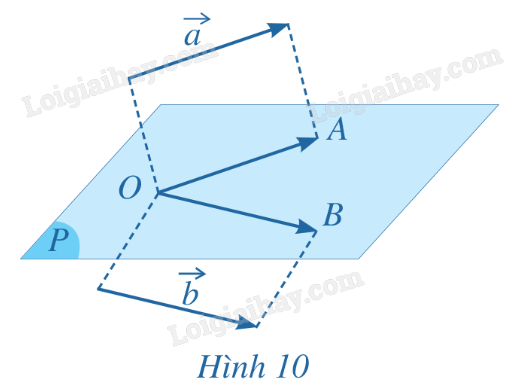
a) Vì M, N lần lượt là trung điểm của các cạnh AD và BC nên \(\overrightarrow {AM}  =  - \overrightarrow {DM} \), \(\overrightarrow {NB}  =  - \overrightarrow {NC} \).

Ta có \(\frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {DC} } \right) = \frac{1}{2}\left( {\overrightarrow {AM}  + \overrightarrow {MN}  + \overrightarrow {NB}  + \overrightarrow {DM}  + \overrightarrow {MN}  + \overrightarrow {NC} } \right)\)

\( = \frac{1}{2}\left( { - \overrightarrow {DM}  + \overrightarrow {MN}  - \overrightarrow {NC}  + \overrightarrow {DM}  + \overrightarrow {MN}  + \overrightarrow {NC} } \right) = \frac{1}{2}.2\overrightarrow {MN}  = \overrightarrow {MN} \) (đpcm).

b) Vì \(\overrightarrow {AM}  =  - \overrightarrow {DM}  \Leftrightarrow \overrightarrow {MA}  + \overrightarrow {MD}  = \overrightarrow 0 \); \(\overrightarrow {NB}  =  - \overrightarrow {NC}  \Leftrightarrow \overrightarrow {NB}  + \overrightarrow {NC}  = \overrightarrow 0 \).

Mặt khác, I là trung điểm của MN nên \(\overrightarrow {IM}  + \overrightarrow {IN}  = \overrightarrow 0 \).

Ta có \(\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  + \overrightarrow {ID} \)

\( = \left( {\overrightarrow {IM}  + \overrightarrow {MA} } \right) + \left( {\overrightarrow {IN}  + \overrightarrow {NB} } \right) + \left( {\overrightarrow {IN}  + \overrightarrow {NC} } \right) + \left( {\overrightarrow {IM}  + \overrightarrow {MD} } \right)\)

\( = \left( {2\overrightarrow {IM}  + 2\overrightarrow {IN} } \right) + \left( {\overrightarrow {MA}  + \overrightarrow {MD} } \right) + \left( {\overrightarrow {NB}  + \overrightarrow {NC} } \right)\)

\( = 2\left( {\overrightarrow {IM}  + \overrightarrow {IN} } \right) + \overrightarrow 0  + \overrightarrow 0  = 2\overrightarrow 0  = \overrightarrow 0 \) (đpcm).

HĐ6

Trả lời câu hỏi Hoạt động 6 trang 61 SGK Toán 12 Cánh diều

Trong không gian, cho hai vecto \(\vec a\), \(\vec b\) khác \(\vec 0\). Lấy một điểm O tùy ý.

a) Vẽ hai vecto \(\overrightarrow {OA}  = \vec a\), \(\overrightarrow {OB}  = \vec b\).

b) Khi đó, hai vecto \(\overrightarrow {OA}\), \(\overrightarrow {OB} \) có giá nằm trong cùng mặt phẳng (P) (Hình 10). Nêu định nghĩa góc giữa hai vecto \(\overrightarrow {OA}\), \(\overrightarrow {OB} \) trong mặt phẳng (P).

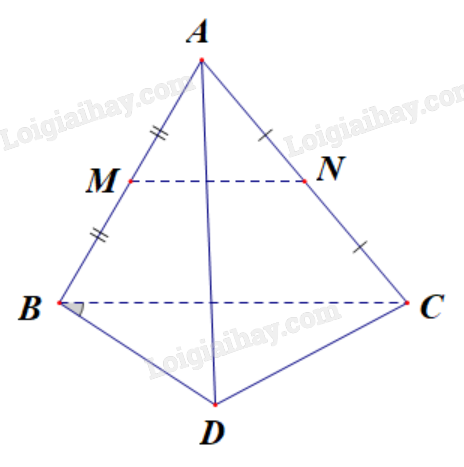
Lời giải chi tiết:

Trong không gian, cho hai vecto \(\vec a, \vec b\) khác \(\vec 0\). Lấy một điểm O tùy ý và vẽ hai vecto \(\overrightarrow {OA}  = \vec a\), \(\overrightarrow {OB}  = \vec b\). Góc giữa hai vecto \(\vec a\), \(\overrightarrow {b} \) trong không gian, ký hiệu \(\left( {\vec a,\vec b} \right)\) là góc giữa hai vecto \(\overrightarrow {OA}\), \(\overrightarrow {OB} \).

LT6

Trả lời câu hỏi Luyện tập 6 trang 61 SGK Toán 12 Cánh diều

Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB, AC. Hãy tính góc giữa hai vecto \(\overrightarrow {MN} \), \(\overrightarrow {BD} \).

Phương pháp giải:

Đưa về tìm góc giữa hai vecto chung gốc.

Lời giải chi tiết:

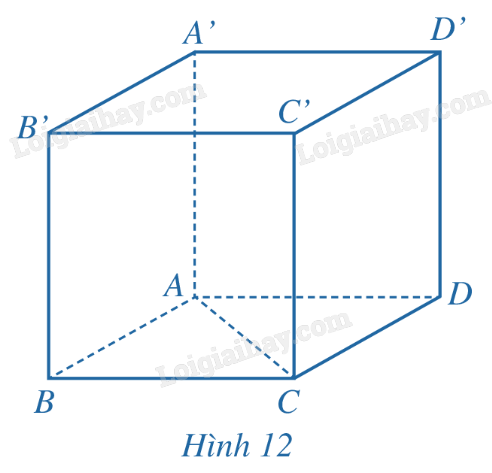
Vì ABCD là tứ diện đều nên tam giác BCD đều, suy ra \(\widehat {CBD} = {60^o}\).

Vì M, N lần lượt là trung điểm các cạnh AB, AC nên MN là đường trung bình của tam giác ABC.

Do đó MN // BC.

Vì \(\overrightarrow {MN} \) và \(\overrightarrow {BC} \) cùng hướng nên \(\left( {\overrightarrow {MN} ,\overrightarrow {BD} } \right) = \left( {\overrightarrow {BC} ,\overrightarrow {BD} } \right) = \widehat {CBD} = {60^o}\).

HĐ7

Trả lời câu hỏi Hoạt động 7 trang 61 SGK Toán 12 Cánh diều

Trong không gian, cho hình lập phương ABCD.A’B’C’D’ có độ dài bằng 3cm (Hình 12).

a) Tính góc giữa hai vecto \(\overrightarrow {AC} \), \(\overrightarrow {A'D'} \).

b) Tính \(\left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {A'D'} } \right|.cos(\overrightarrow {AC} ,\overrightarrow {A'D'} \)).

Phương pháp giải:

Áp dụng quy tắc 3 điểm và vecto trong không gian.

Lời giải chi tiết:

Ta có A’D’ // AD, suy ra góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {A'D'}\) chính là góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {AD} \) hay \(\widehat {CAD}\).

a) ABCD là hình vuông nên \(\widehat {CAD} = 45^\circ \).

b) \(\overrightarrow {\left| {AC} \right|} .|\overrightarrow {A'D'|} = AC.AD = 3.3 = 9\).

\(cos(\overrightarrow {AC} ,\overrightarrow {A'D'}) = cos(\overrightarrow {AC} ,\overrightarrow {AD} )\)

\(= \frac{{\overrightarrow {AC} .\overrightarrow {AD} }}{{\overrightarrow {\left| {AC} \right|} .\overrightarrow {\left| {AD} \right|} }} = \frac{{3.3}}{{3.3}} = 1\).

LT7

Trả lời câu hỏi Luyện tập 7 trang 62 SGK Toán 12 Cánh diều

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính \(\overrightarrow {A'B} .\overrightarrow {D'C'} \); \(\overrightarrow {D'A} .\overrightarrow {BC} \).

Phương pháp giải:

Áp dụng công thức \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).

Lời giải chi tiết:

* Tính \(\overrightarrow {A'B} .\overrightarrow {D'C'} \).

Ta có \(\overrightarrow {D'C'}  = \overrightarrow {A'B'} \) nên \(\left( {\overrightarrow {A'B} ,\overrightarrow {D'C'} } \right) = \left( {\overrightarrow {A'B} ,\overrightarrow {A'B'} } \right) = \widehat {BA'B'} = {45^o}\) (vì ABB’A’ là hình vuông).

Mặt khác, A’B là đường chéo hình vuông cạnh a nên \(A'B = a\sqrt 2 \).

Do đó \(\overrightarrow {A'B} .\overrightarrow {D'C'}  = A'B.D'C'.\cos \left( {\overrightarrow {A'B} ,\overrightarrow {D'C'} } \right)\)

\( = A'B.D'C'.\cos \widehat {BA'B'} = a\sqrt 2 .a.\cos {45^o} = {a^2}\).

* Tính \(\overrightarrow {D'A} .\overrightarrow {BC} \).

Ta có \(\overrightarrow {D'A} .\overrightarrow {BC}  =  - \overrightarrow {AD'} .\overrightarrow {BC} \).

Mặt khác \(\overrightarrow {AD'}  = \overrightarrow {BC'} \) nên \(\left( {\overrightarrow {AD'} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {BC'} ,\overrightarrow {BC} } \right) = \widehat {CBC'} = {45^o}\) (vì BCC’B’ là hình vuông).

Do đó \(\overrightarrow {D'A} .\overrightarrow {BC}  =  - \overrightarrow {AD'} .\overrightarrow {BC}  =  - AD'.BC.\cos \left( {\overrightarrow {AD'} ,\overrightarrow {BC} } \right)\)

\( =  - a\sqrt 2 .a.\cos {45^o} =  - {a^2}\).