Giải mục 1 trang 76, 77 SGK Toán 12 tập 2 - Chân trời sáng tạo

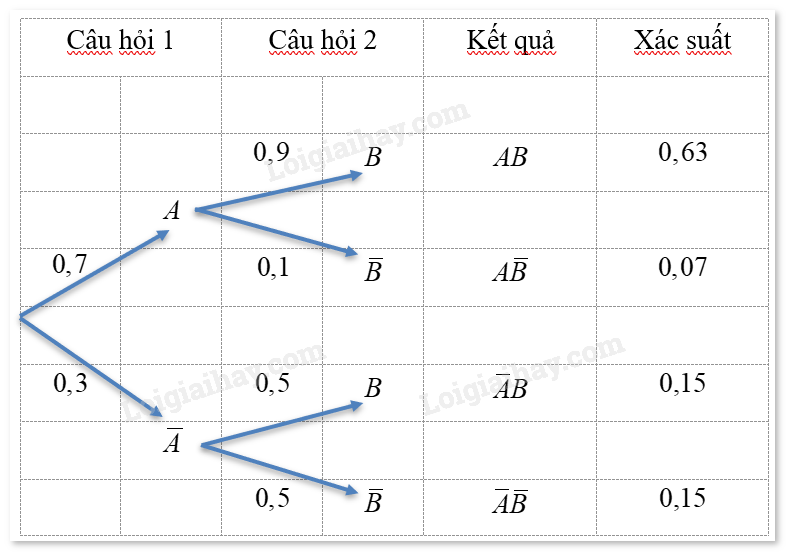
HĐ1

Trả lời câu hỏi Hoạt động 1 trang 76 SGK Toán 12 Chân trời sáng tạo

Chị An trả lời hai câu hỏi. Xác suất trả lời đúng câu hỏi thứ nhất là 0,7. Xác suất trả lời đúng câu hỏi thứ hai là 0,9 nếu chị An trả lời đúng câu hỏi thứ nhất và là 0,5 nếu chị An không trả lời đúng câu hỏi thứ nhất.

Gọi \(A\) là biến cố “Chị An trả lời đúng câu hỏi thứ nhất” và B là biến cố “Chị An trả lời đúng câu hỏi thứ hai”. Hãy tìm các giá trị thích hợp điền vào các ô ? ở sơ đồ hình cây sau:

Phương pháp giải:

Từ sơ đồ hình cây, sau đó điền vào dấu ?

Lời giải chi tiết:

Do xác suất chị An trả lời đúng câu hỏi thứ nhất là 0,7 nen xác suất chị An trả lời sai câu hỏi thứ nhất là \(1 - 0,7 = 0,3\), suy ra \(P\left( {\bar A} \right) = 0,3\)

Với trường hợp chị An trả lời đúng câu thứ nhất, xác suất chị trả lời đúng câu thứ hai là 0,9. Suy ra xác suất chị trả lời sai câu thứ hai là \(P\left( {\bar B|A} \right) = 1 - 0,9 = 0,1.\)

Suy ra \(P\left( {A\bar B} \right) = 0,7.0,1 = 0,07\).

Với trường hợp chị An trả lời sai câu thứ nhất, xác suất chị trả lời đúng câu thứ hai là 0,5. Suy ra xác suất chị trả lời sai câu thứ hai là \(P\left( {\bar B|\bar A} \right) = 1 - 0,5 = 0,5\).

Suy ra \(P\left( {\bar A\bar B} \right) = 0,3.0,5 = 0,15\). Ta có sơ đồ hình cây hoàn thiện sau:

TH1

Trả lời câu hỏi Thực hành 1 trang 77 SGK Toán 12 Chân trời sáng tạo

Vào mỗi buổi sáng ở tuyến phố H, xác suất xảy ra tắc đường khi trời mưa và không mưa lần lượt là 0,7 và 0,2. Xác suất có mưa vào một buổi sáng là 0,1. Tính xác suất để sáng đó tuyến phố H bị tắc đường.

Phương pháp giải:

Gọi \(A\) là biến cố “Tuyến phố H bị tắc đường”, \(B\) là biến cố “Sáng hôm đó trời mưa”. Để tính xác suất để sáng đó tuyến phố H bị tắc đường, ta cần sử dụng công thức xác suất toàn phần \(P\left( A \right) = P\left( B \right)P\left( {A|B} \right) + P\left( {\bar B} \right)P\left( {A|\bar B} \right)\).

Lời giải chi tiết:

Gọi \(A\) là biến cố “Tuyến phố H bị tắc đường”, \(B\) là biến cố “Sáng hôm đó trời mưa”.

Theo đề bài, ta có \(P\left( B \right) = 0,1\); \(P\left( {A|B} \right) = 0,7\) và \(P\left( {A|\bar B} \right) = 0,2\).

Ta có \(P\left( {\bar B} \right) = 1 - P\left( B \right) = 1 - 0,1 = 0,9.\)

Như vậy, xác suất để sáng hôm đó tuyến phố H bị tắc đường là

\(P\left( A \right) = P\left( B \right)P\left( {A|B} \right) + P\left( {\bar B} \right)P\left( {A|\bar B} \right) = 0,1.0,7 + 0,9.0,2 = 0,25.\)