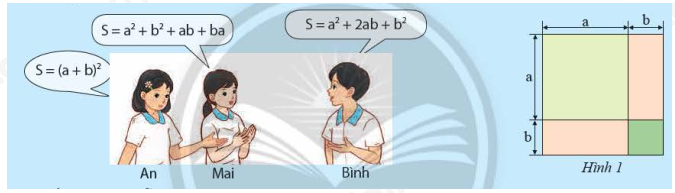
Giải mục 1 trang 19, 20 SGK Toán 8 tập 1– Chân trời sáng tạoa) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích (S) của các phần tô màu trong Hình 1 như sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
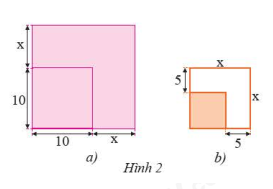
HĐ1 Video hướng dẫn giải a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích \(S\) của các phần tô màu trong Hình 1 như sau: Kết quả của mỗi bạn có đúng không? Giải thích. b) Thực hiện phép nhân và rút gọn đa thức của bạn An. c) Bằng cách làm tương tự ở câu b), có thể biến đổi biểu thức \({\left( {a - b} \right)^2}\) thành biểu thức nào? Phương pháp giải: Áp dụng quy tắc nhân đa thức. Lời giải chi tiết: a) Chiều dài và chiều rộng của hình 1 lần lượt là \(a + b\), \(a + b\) Tổng diện tích \(S\) của hình 1 là: \(S = \left( {a + b} \right)\left( {a + b} \right) = a.a + ab + ba + b.b = {a^2} + ab + ba + {b^2} = {a^2} + 2ab + {b^2}\) hay \(S = {\left( {a + b} \right)^2} = {a^2} + {b^2} + ab + ba = {a^2} + 2ab + {b^2}\) Vậy cả ba bạn An, Mai và Bình đều nói đúng kết quả. b) \(S = {\left( {a + b} \right)^2} = \left( {a + b} \right)\left( {a + b} \right) = a.a + ab + ba + b.b = {a^2} + 2ab + {b^2}\) c) Ta có: \({\left( {a - b} \right)^2} = \left( {a - b} \right)\left( {a - b} \right) = a.a - ab - ba + b.b = {a^2} - 2ab + {b^2}\) Thực hành 1 Video hướng dẫn giải Tính: a) \({\left( {3x + 1} \right)^2}\) b) \({\left( {4x + 5y} \right)^2}\) c) \({\left( {5x - \dfrac{1}{2}} \right)^2}\) d) \({\left( { - x + 2{y^2}} \right)^2}\) Phương pháp giải: Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu \(\begin{array}{l}{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\\{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\end{array}\) Lời giải chi tiết: a) \({\left( {3x + 1} \right)^2} = {\left( {3x} \right)^2} + 2.3x.1 + {1^2} = 9{x^2} + 6x + 1\) b) \({\left( {4x + 5y} \right)^2} = {\left( {4x} \right)^2} + 2.4x.5y + {\left( {5y} \right)^2} = 16{x^2} + 40xy + 25{y^2}\) c) \({\left( {5x - \dfrac{1}{2}} \right)^2} = {\left( {5x} \right)^2} - 2.5x.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2} = 25{x^2} - 5x + \dfrac{1}{4}\) d) \({\left( { - x + 2{y^2}} \right)^2} = {\left( { - x} \right)^2} + 2.\left( { - x} \right).\left( {2{y^2}} \right) + {\left( {2{y^2}} \right)^2} = {x^2} - 4x{y^2} + 4{y^4}\) Thực hành 2 Video hướng dẫn giải Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu: a) \({a^2} + 10ab + 25{b^2}\) b) \(1 + 9{a^2} - 6a\) Phương pháp giải: Đưa biểu thức về dạng vế phải của hai hằng đẳng thức: Bình phương của một tổng, một hiệu \(\begin{array}{l}{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\\{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\end{array}\) Lời giải chi tiết: a) \({a^2} + 10ab + 25{b^2} = {a^2} + 2.a.5b + {\left( {5b} \right)^2} = {\left( {a + 5b} \right)^2}\) b) \(1 + 9{a^2} - 6a = 1 - 6a + 9{a^2} = 1 - 2.1.3a + {\left( {3a} \right)^2} = {\left( {1 - 3a} \right)^2}\) Thực hành 3 Video hướng dẫn giải Tính nhanh: a) \({52^2}\) b) \({98^2}\) Phương pháp giải: Tách số đã cho thành tổng hoặc hiệu của một số tròn chục với một số tự nhiên. Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu Lời giải chi tiết: a) \({52^2} = {\left( {50 + 2} \right)^2} = {50^2} + 2.50.2 + {2^2} = 2500 + 200 + 4 = 2704\) b) \({98^2} = {\left( {100 - 2} \right)^2} = {100^2} - 2.100.2 + {2^2} = 10000 - 400 + 4 = 9604\) Vận dụng 1 Video hướng dẫn giải a) Một mảnh vườn hình vuông có cạnh \(10\)m được mở rộng cả hai cạnh thêm \(x\) (m) như Hình 2a. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn sau khi mở rộng. b) Một mảnh vườn hình vuông sau khi mở rộng mỗi cạnh \(5\)m thì được một mảnh vườn hình vuông có cạnh là \(x\) (m) như Hình 2b. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn trước khi mở rộng. Phương pháp giải: Áp dụng công thức tính diện tích hình vuông Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu. Lời giải chi tiết: a) Độ dài cạnh mảnh vườn hình vuông sau khi mở rộng là: \(x + 10\) (m) Diện tích mảnh vườn sau khi mở rộng là: \(\left( {x + 10} \right)\left( {x + 10} \right) = {\left( {x + 10} \right)^2} = {x^2} + 2.x.10 + {10^2} = {x^2} + 20x + 100\) (\({m^2}\)) b) Độ dài cạnh mảnh vườn hình vuông trước khi mở rộng là: \(x - 5\) (m) Diện tích mảnh vườn hình vuông trước khi mở rộng là: \(\left( {x - 5} \right)\left( {x - 5} \right) = {\left( {x - 5} \right)^2} = {x^2} - 2.x.5 + {5^2} = {x^2} - 10x + 25\) (\({m^2}\))
|




















Danh sách bình luận