Giải mục 2 trang 20 SGK Toán 8 tập 1– Chân trời sáng tạo

HĐ2

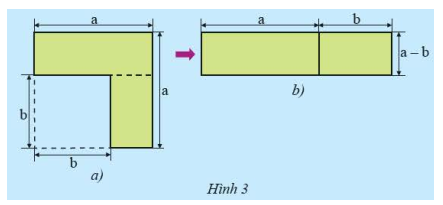
a) Từ Hình 3a, người ta cắt ghép tạo thành Hình 3b. Viết hai biểu thức khác nhau, mỗi biểu thức biểu thị diện tích (phần tô màu) của một trong hai hình bên.

b) Thực hiện phép nhân và rút gọn đa thức, biến đổi biểu thức \(\left( {a + b} \right)\left( {a - b} \right)\) thành một đa thức thu gọn. Từ đó, có kết luận gì về diện tích của hai hình bên?

Phương pháp giải:

a) Áp dụng công thức tính diện tích hình vuông

b) Áp dụng công thức tính diện tích hình chữ nhật, quy tắc nhân đa thức.

Lời giải chi tiết:

a) Diện tích Hình 3a là: \({a^2} - {b^2}\)

Diện tích Hình 3b là: \(\left( {a + b} \right)\left( {a - b} \right)\)

b) Ta có: \(\left( {a + b} \right)\left( {a - b} \right) = a.a - ab + ba - {b^2} = {a^2} - ab + ab - {b^2} = {a^2} - {b^2}\)

Suy ra: \(\left( {a + b} \right)\left( {a - b} \right) = {a^2} - {b^2}\)

Vậy diện tích của hai hình bằng nhau.

Thực hành 4

Thực hiện các phép nhân:

a) \(\left( {4 - x} \right)\left( {4 + x} \right)\)                                   

b) \(\left( {2y + 7z} \right)\left( {2y - 7z} \right)\)                      

c) \(\left( {x + 2{y^2}} \right)\left( {x - 2{y^2}} \right)\)

Phương pháp giải:

Áp dụng hằng đẳng thức: Hiệu của hai bình phương.

Lời giải chi tiết:

a) \(\left( {4 - x} \right)\left( {4 + x} \right) = {4^2} - {x^2} = 16 - {x^2}\)

b) \(\left( {2y + 7z} \right)\left( {2y - 7z} \right) = {\left( {2y} \right)^2} - {\left( {7z} \right)^2} = 4{y^4} - 49{z^2}\)

c) \(\left( {x + 2{y^2}} \right)\left( {x - 2{y^2}} \right) = {x^2} - {\left( {2{y^2}} \right)^2} = {x^2} - 4{y^4}\)

Thực hành 5

Tính nhanh:

a) \(82.78\)                                          

b) \(87.93\)                             

c) \({125^2} - {25^2}\)

Phương pháp giải:

Đưa tích của hai thừa số về dạng tích của một tổng và một hiệu rồi áp dụng hằng đẳng thức: Hiệu của hai bình phương.

Lời giải chi tiết:

a) \(82.78 = \left( {80 + 2} \right)\left( {80 - 2} \right) = {80^2} - {2^2} = 6400 - 4 = 6396\)

b) \(87.93 = \left( {90 - 3} \right)\left( {90 + 3} \right) = {90^2} - {3^2} = 8100 - 9 = 8091\)

c) \({125^2} - {25^2} = \left( {125 + 25} \right)\left( {125 - 25} \right) = 150.100 = 15000\)

Vận dụng 2

Giải đáp câu hỏi ở đầu bài (trang 18)

Phương pháp giải:

Áp dụng hằng đẳng thức: Hiệu của hai bình phương

Lời giải chi tiết:

Ta có:

\({65^2} - {35^2} = \left( {65 + 35} \right)\left( {65 - 35} \right) = 100.30 = 3000\)

\(102.98 = \left( {100 + 2} \right)\left( {100 - 2} \right) = {100^2} - {2^2} = 10000 - 4 = 9996\)