Giải mục 1 trang 10, 11, 12 SGK Toán 9 tập 1 - Chân trời sáng tạoĐể chuyển đổi từ độ F ( kí hiệu x) sang độ C (ký hiệu y), ta dùng công thức: (y = frac{5}{9}(x - 32)) a) Biến đổi công thức trên về dạng x – 1,8y = 32. (1) b) Hỏi 20oC tương ứng bao nhiêu độ F? c) Hỏi 98,6oF tương ứng bao nhiêu độ C? Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
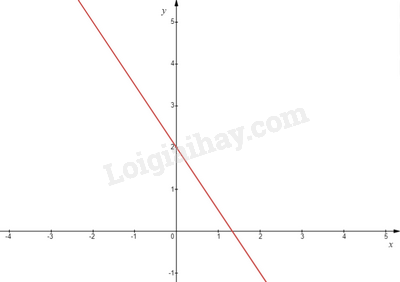
HĐ1 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 1 trang 10 SGK Toán 9 Chân trời sáng tạo Để chuyển đổi từ độ F ( kí hiệu x) sang độ C (ký hiệu y), ta dùng công thức: \(y = \frac{5}{9}(x - 32)\) a) Biến đổi công thức trên về dạng x – 1,8y = 32.(1) b) Hỏi 20oC tương ứng bao nhiêu độ F? c) Hỏi 98,6oF tương ứng bao nhiêu độ C? Phương pháp giải: - Biến đổi cho x,y về cùng 1 vế, hằng số 1 vế - Rút x theo y thay vào tính ra kết quả rồi kết luận - Rút y theo x thay vào tính ra kết quả rồi kết luận Lời giải chi tiết: a) Ta có \(y = \frac{5}{9}(x - 32)\) \(9y = 5(x - 32)\) \(\begin{array}{l}5x - 9y = 160\\x - 1,8y = 32\end{array}\) b) x – 1,8y = 32 \(\begin{array}{l}x = 32 + 1,8y\\x = 32 + 1,8.20\\x = 68\end{array}\) Vậy 20oC tương ứng 68oF. c) Ta có \(y = \frac{5}{9}(x - 32)\) \(y = \frac{5}{9}(98,6 - 32) = 37\) Vậy 98,6oF tương ứng 37oC. TH1 Video hướng dẫn giải Trả lời câu hỏi Thực hành 1 trang 12 SGK Toán 9 Chân trời sáng tạo Xác định các hệ số a, b, c của mỗi phương trình bậc nhất hai ẩn sau: a) x + 5y = -4 b) \(\sqrt 3 x + y = 0\) c) \(0x - \frac{3}{2}y = 6\) d) 2x + 0y = - 1,5. Phương pháp giải: Dựa vào khái niệm phương trình bậc nhất hai ẩn x và y là hệ thức có dạng \(ax + by = c\) Trong đó, a và b không đồng thời bằng 0. Lời giải chi tiết: a) a = 1; b = 5; c = -4 b) a = \(\sqrt 3 \); b = 1; c = 0 c) a = 0; b = \( - \frac{3}{2}\); c = 6 d) a = 2; b = 0; c = - 1,5. TH2 Video hướng dẫn giải Trả lời câu hỏi Thực hành 2 trang 12 SGK Toán 9 Chân trời sáng tạo Cho phương trình 3x + 2y = 4. (1) a) Trong 2 cặp số (1;2) và (2;-1), cặp số nào là nghiệm của phương trình(1)? b) Tìm yo để cặp số (4;yo) là nghiệm của phương trình (1). c) Tìm thêm 2 nghiệm của phương trình (1). d) Hãy biểu diễn tất cả các nghiệm của phương trình (1) trên mặt phẳng toạ độ Oxy. Phương pháp giải: - Thay lần lượt 2 cặp số vào phương trình (1) cái nào thoả mãn thì chính là nghiệm. - Thay x = 4 và phương trình để tìm ra yo. - Cho x bất kì rồi tìm ra y - Dựa vào VD3 trang 11 để vẽ các nghiệm trên mặt phẳng toạ độ Oxy. Lời giải chi tiết: a) Thay cặp số (1;2) vào (1) ta có: 3.1 + 2.2 = 7 \( \ne \) VP. Vậy (1;2) không phải nghiệm của (1) Thay cặp số (2;-1) vào (1) ta có: 3.2 + 2.(-1) = 4 = VP. Vậy (2;-1) là nghiệm của (1). b) Thay x = 4 vào (1) ta có: 3.4 + 2y = 4 Suy ra \({y_o} = \frac{{4 - 12}}{2} = - 4\). c) Ta có \(\begin{array}{l}3x + 2y = 4\\y = \frac{{4 - 3x}}{2}\end{array}\) Cho x = 0 suy ra \(y = 2\). Vậy (0;2) là nghiệm của phương trình (1). Cho x = 1 suy ra \(y = \frac{1}{2}\). Vậy (1; \(\frac{1}{2}\)) là nghiệm của phương trình (1). d) Viết lại phương trình thành \(y = \frac{{4 - 3x}}{2} = 2 - \frac{3}{2}x\). Từ đó, tất cả các nghiệm đã cho được biểu diễn bởi đường thẳng d: \(y = 2 - \frac{3}{2}x\).
|




















Danh sách bình luận