Giải bài tập 8 trang 79 SGK Toán 12 tập 1 - Cánh diềuTính (mathop {{F_1}}limits^ to ,mathop {{F_2}}limits^ to ,mathop {{F_3}}limits^ to ) theo hằng số c dựa vào các vecto (mathop {SR}limits^ to ,mathop {SQ}limits^ to ,mathop {SP}limits^ to ). Sử dụng công thức (mathop {{F_1}}limits^ to + mathop {{F_2}}limits^ to + mathop {{F_3}}limits^ to = mathop Flimits^ to ) tìm c rồi thay ngược lại vào các vecto. Quảng cáo
Đề bài
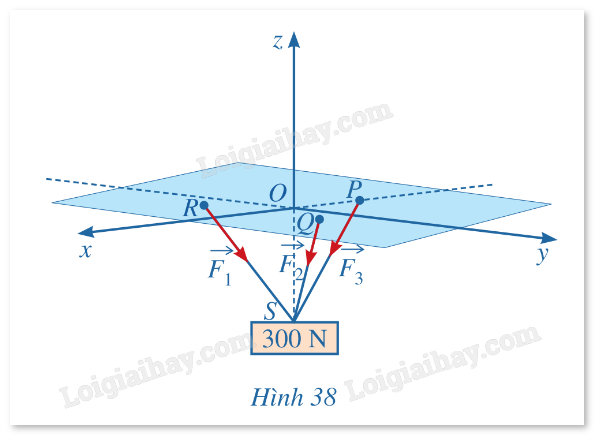
Một vật có trọng lượng 300N được treo bằng ba sợi dây cáp không dãn có chiều dài bằng nhau, mỗi dây cáp có một đầu được gắn tại một trog các điểm \(P( - 2;0;0),Q(1;\sqrt 3 ;0),R(1; - \sqrt 3 ;0)\) còn đầu kia gắn với vật tại điểm \(S(0;0; - 2\sqrt 3 )\) như Hình 38. Gọi \(\mathop {{F_1}}\limits^ \to ,\mathop {{F_2}}\limits^ \to ,\mathop {{F_3}}\limits^ \to \) lần lượt là lực căng trên các sợi dây cáp RS, QS và PS. Tìm tọa độ các lực \(\mathop {{F_1}}\limits^ \to ,\mathop {{F_2}}\limits^ \to ,\mathop {{F_3}}\limits^ \to \).\(\)
Phương pháp giải - Xem chi tiết Tính \(\mathop {{F_1}}\limits^ \to ,\mathop {{F_2}}\limits^ \to ,\mathop {{F_3}}\limits^ \to \) theo hằng số c dựa vào các vecto \(\mathop {SR}\limits^ \to ,\mathop {SQ}\limits^ \to ,\mathop {SP}\limits^ \to \). Sử dụng công thức \(\mathop {{F_1}}\limits^ \to + \mathop {{F_2}}\limits^ \to + \mathop {{F_3}}\limits^ \to = \mathop F\limits^ \to \) tìm c rồi thay ngược lại vào các vecto. Lời giải chi tiết Ta có: \(\mathop {SP}\limits^ \to = ( - 2;0;2\sqrt 3 ),\mathop {SQ}\limits^ \to = (1;\sqrt 3 ;2\sqrt 3 ),\mathop {SR}\limits^ \to = (1; - \sqrt 3 ;2\sqrt 3 )\). Suy ra: \(\left| {\mathop {SP}\limits^ \to } \right| = \left| {\mathop {SQ}\limits^ \to } \right| = \left| {\mathop {SR}\limits^ \to } \right| = 4\). Mặt khác: \(\mathop {SP}\limits^ \to = (3;\sqrt 3 ;0),\mathop {QR}\limits^ \to = (0; - 2\sqrt 3 ;0),\mathop {SR}\limits^ \to = ( - 3;\sqrt 3 ;0)\). Suy ra: \(\left| {\mathop {QP}\limits^ \to } \right| = \left| {\mathop {QR}\limits^ \to } \right| = \left| {\mathop {RP}\limits^ \to } \right| = 2\sqrt 3 \) nên tam giác PQR đều. Do đó: \(\left| {\mathop {{F_1}}\limits^ \to } \right| = \left| {\mathop {{F_2}}\limits^ \to } \right| = \left| {\mathop {{F_3}}\limits^ \to } \right|\). Tồn tại hằng số \(c \ne 0\) sao cho: \(\mathop {{F_1}}\limits^ \to = c\mathop {SR}\limits^ \to = (c; - \sqrt 3 c;2\sqrt 3 c)\) \(\mathop {{F_2}}\limits^ \to = c\mathop {SQ}\limits^ \to = (c;\sqrt 3 c;2\sqrt 3 c)\) \(\mathop {{F_3}}\limits^ \to = c\mathop {SP}\limits^ \to = ( - 2c;0;2\sqrt 3 c)\) Suy ra \(\mathop {{F_1}}\limits^ \to + \mathop {{F_2}}\limits^ \to + \mathop {{F_3}}\limits^ \to = (0;0;6\sqrt 3 c)\). Mà \(\mathop {{F_1}}\limits^ \to + \mathop {{F_2}}\limits^ \to + \mathop {{F_3}}\limits^ \to = \mathop F\limits^ \to \), trong đó \(\mathop F\limits^ \to = (0;0; - 300)\) là trọng lực của vật. Suy ra \(6\sqrt 3 c = - 300\), tức \(c = \frac{{ - 50\sqrt 3 }}{3}\). Vậy \(\mathop {{F_1}}\limits^ \to = \left( {\frac{{ - 50\sqrt 3 }}{3};50; - 100} \right),\mathop {{F_2}}\limits^ \to = \left( {\frac{{ - 50\sqrt 3 }}{3}; - 50; - 100} \right);\mathop {{F_1}}\limits^ \to = \left( {\frac{{100\sqrt 3 }}{3};0; - 100} \right)\).
|




















Danh sách bình luận