Giải bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạoCho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11). a) Chứng minh 2AD = AB + AC – BC. b) Tìm các hệ thức tương tự như ở câu a. Tổng hợp đề thi giữa kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên Quảng cáo
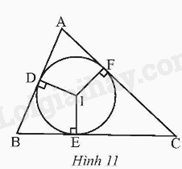
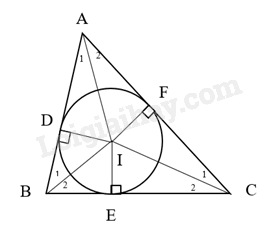
Đề bài Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11). a) Chứng minh 2AD = AB + AC – BC. b) Tìm các hệ thức tương tự như ở câu a.
Phương pháp giải - Xem chi tiết - Đọc kĩ dữ kiện đề bài để vẽ hình. - Chứng minh \(\Delta \) ADI = \(\Delta \) AFI (c – g – c) nên AD = AF. Tương tự, \(\Delta \)DBI = \(\Delta \)EIB (c – g – c) nên BD = BE (hai cạnh tương ứng); \(\Delta \)FCI = \(\Delta \)ECI (c – g – c) nên FC = EC rồi thay vào hệ thức 2AD = AB + AC – BC để chứng minh. Lời giải chi tiết
a) Vì I là tâm đường tròn nội tiếp tam giác ABC Suy ra I là giao điểm của ba đường phân giác tam giác ABC \(\widehat {{A_1}} = \widehat {{A_2}};\widehat {{B_1}} = \widehat {{B_2}};\widehat {{C_1}} = \widehat {{C_2}}\). Xét \(\Delta \)ADI và \(\Delta \)AFI có: ID = IF = R; \(\widehat {{A_1}} = \widehat {{A_2}}\) (chứng minh trên); AI chung. Suy ra \(\Delta \)ADI = \(\Delta \)AFI (c – g – c). Do đó, AD = AF (hai cạnh tương ứng) (1). Chứng minh tương tự, ta được: \(\Delta \)DBI = \(\Delta \)EIB (c – g – c) suy ra BD = BE (hai cạnh tương ứng) (2). \(\Delta \)FCI = \(\Delta \)ECI (c – g – c) suy ra FC = EC (hai cạnh tương ứng) (3). - Ta có: AB + AC – BC = AD + BD + AF + FC – BE – EC (4). Thay (1), (2), (3) vào (4) ta được: AB + AC – BC = AD + BE + AD + EC – BE – EC = 2AD (điều phải chứng minh). b) Các hệ thức tương tự như ở câu a: 2AF = AB + AC – BC; 2BD = 2BE = AB + BC – AC; 2EC = 2FC = AC + BC – AB.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
