Giải bài tập 1.13 trang 19 SGK Toán 12 tập 1 - Kết nối tri thứcTrong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất. Quảng cáo
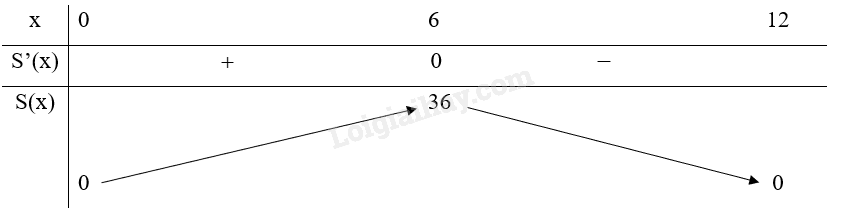
Đề bài Trong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất. Phương pháp giải - Xem chi tiết Sử dụng kiến thức về cách tìm giá trị lớn nhất của hàm số trên một đoạn để tính: Giả sử \(y = f\left( x \right)\) là hàm số liên tục trên \(\left[ {a;b} \right]\) và có đạo hàm trên (a; b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn \(\left[ {a;b} \right]\) mà đạo hàm \(f'\left( x \right) = 0\). Các bước tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {a;b} \right]\): 1. Tìm các điểm \({x_1},{x_2},...{x_n} \in \left( {a;b} \right)\), tại đó \(f'\left( x \right) = 0\) hoặc không tồn tại. 2. Tính \(f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right)\), f(a) và f(b). 3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có: \(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\) Lời giải chi tiết Gọi chiều dài của hình chữ nhật là x (cm, \(0 < x < 12\)) Chiều rộng của hình chữ nhật là \(12 - x\left( {cm} \right)\) Diện tích của hình chữ nhật là: \(x\left( {12 - x} \right) = - {x^2} + 12x\;\left( {c{m^2}} \right)\) Đặt \(S\left( x \right) = - {x^2} + 12x,x \in \left( {0;12} \right)\) \(S'\left( x \right) = - 2x + 12,S'\left( x \right) = 0 \Leftrightarrow x = 6\left( {tm} \right)\) Bảng biến thiên:
Do đó, trong các hình có cùng chu vi thì hình chữ nhật có diện tích lớn nhất là \(36c{m^2}\).
|




















Danh sách bình luận