Giải bài 9 trang 89 vở thực hành Toán 9Cho tam giác ABC vuông ở A và BD là tia phân giác góc B. Biết (widehat C = {42^o},AB = 22), tính độ dài BD, AD, DC (làm tròn đến chữ số thập phân thứ nhất). Quảng cáo
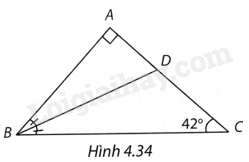
Đề bài Cho tam giác ABC vuông ở A và BD là tia phân giác góc B. Biết \(\widehat C = {42^o},AB = 22\), tính độ dài BD, AD, DC (làm tròn đến chữ số thập phân thứ nhất). Phương pháp giải - Xem chi tiết + Tam giác ABC vuông tại A nên \(\widehat B = {90^o} - \widehat C\) + Vì BD là tia phân giác góc B nên \(\widehat {ABD} = \frac{{\widehat {ABC}}}{2}\) + Tam giác ABD vuông ở A, ta có: \(\cos \widehat {ABD} = \frac{{AB}}{{BD}}\) tính được BD, \(\tan \widehat {ABD} = \frac{{AD}}{{AB}}\) tính được AD + Tam giác ABC vuông tại A nên\(\tan C = \frac{{AB}}{{AC}}\), tính được AC. + Từ đó, \(DC = AC - AD\) Lời giải chi tiết (H.4.34)
Tam giác ABC vuông ở A nên \(\widehat B = {90^o} - \widehat C = {48^o}\) Vì BD là tia phân giác góc B nên \(\widehat {ABD} = \frac{{\widehat {ABC}}}{2} = \frac{{{{48}^o}}}{2} = {24^o}\) Tam giác ABD vuông ở A, ta có: \(\cos \widehat {ABD} = \frac{{AB}}{{BD}}\) nên \(BD = \frac{{AB}}{{\cos \widehat {ABD}}} = \frac{{22}}{{\cos {{24}^o}}} \approx 24,1\) \(\tan \widehat {ABD} = \frac{{AD}}{{AB}}\) nên \(AD = AB.\tan \widehat {ABD} = 22.\tan {24^o} \approx 9,8\) Ta có \(\tan C = \frac{{AB}}{{AC}}\) nên \(AC = \frac{{AB}}{{\tan C}} = \frac{{22}}{{\tan {{42}^o}}} \approx \frac{{22}}{{0,9}} \approx 24,4\) Từ đó, \(DC = AC - AD = 24,4 - 9,8 = 14,6\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
