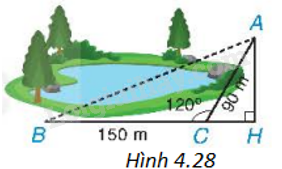
Giải bài 5 trang 87 vở thực hành Toán 9Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là (CA = 90m,CB = 150m) và (widehat {ACB} = {120^o}) (H.4.28). Hãy tính AB giúp bạn. Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Quảng cáo
Đề bài Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là \(CA = 90m,CB = 150m\) và \(\widehat {ACB} = {120^o}\) (H.4.28). Hãy tính AB giúp bạn.
Phương pháp giải - Xem chi tiết + Kẻ đường cao AH của tam giác ABC thì C nằm giữa B và H. + \(\widehat {ACH} = {180^o} - \widehat {ACB} = {60^o}\) + Trong tam giác ACH vuông tại H nên \(HC = AC.\cos \widehat {ACH}\), tính được HC, \(AH = AC.\sin \widehat {ACH}\) tính được AH. + \(BH = BC + CH\) + Áp dụng định lí Pythagore vào tam giác ABH vuông tại H, tính được AB. Lời giải chi tiết Kẻ đường cao AH của tam giác ABC thì C nằm giữa B và H. Trong tam giác ACH, ta có \(\widehat {ACH} = {180^o} - \widehat {ACB} = {60^o}\), \(HC = AC.\cos \widehat {ACH} = 90.\cos {60^o} = 45\left( m \right)\) \(AH = AC.\sin \widehat {ACH} = 90.\sin {60^o} = 45\sqrt 3 \left( m \right)\) Từ đó, \(BH = BC + CH = 150 + 45 = 195\left( m \right)\) \(A{B^2} = B{H^2} + A{H^2} = {195^2} + {\left( {45\sqrt 3 } \right)^2}\) suy ra \(AB = 210\left( m \right)\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
