Giải bài 4 trang 86 vở thực hành Toán 9Tính các số liệu còn thiếu (dấu “?”) ở Hình 4.26 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất. Quảng cáo
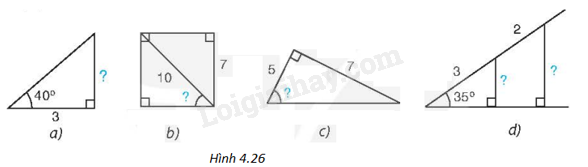
Đề bài Tính các số liệu còn thiếu (dấu “?”) ở Hình 4.26 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.
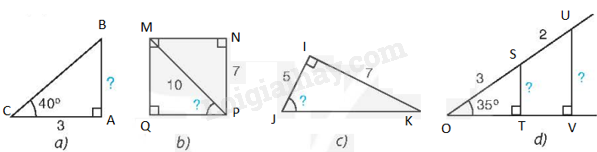
Phương pháp giải - Xem chi tiết a) Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối. b, Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có, tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \). c) Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có, tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \). d) Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề. Lời giải chi tiết (H.4.27) Ta đặt tên các điểm như trong Hình 4.27.
Ở hình a): Trong tam giác ABC vuông tại A, theo định lí về hai cạnh góc vuông, ta có \(AB = AC.\tan C = 3.\tan {40^o} \approx 2,6\) Ở hình b): Ta có: \(QM = NP = 7\) Trong tam giác MPQ vuông tại Q, ta có \(\sin \widehat {MPQ} = \frac{{QM}}{{MP}} = \frac{7}{{10}}\) nên \(\widehat {MPQ} \approx {44^o}\). Ở hình c): Trong tam giác IJK vuông tại I, ta có \(\tan \widehat {IJK} = \frac{{IK}}{{IJ}} = \frac{7}{5}\) nên \(\widehat {IJK} \approx {54^o}\). Ở hình d): Trong tam giác OST vuông tại T, ta có \(\sin {35^o} = \sin \widehat {SOT} = \frac{{ST}}{{OS}}\) nên \(ST = OS.\sin \widehat {SOT} = 3.\sin {35^o} \approx 1,7\). Trong tam giác OUV vuông tại V, ta có \(OU = OS + SU = 3 + 2 = 5\) \(\sin {35^o} = \sin \widehat {UOV} = \frac{{UV}}{{OU}}\) nên \(UV = OU.\sin \widehat {UOV} = 5.\sin {35^o} \approx 2,9\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
