Giải bài 8 trang 37 sách bài tập toán 12 - Chân trời sáng tạo

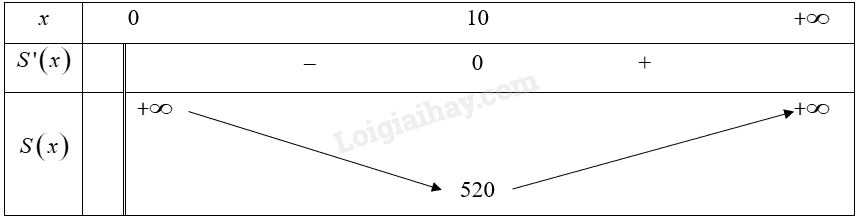
Đề bài

Người ta muốn chế tạo một chiếc hộp hình hộp chữ nhật có thể tích 800 cm với yêu cầu dùng ít vật liệu nhất.

Chiều cao hộp là 8 cm, các kích thước khác là \(x\) (cm), \(y\) (cm) với \(x > 0\) và \(y > 0\).

a) Chứng tỏ rằng \(y = \frac{{100}}{x}\).

b) Tìm diện tích toàn phần \(S\left( x \right)\) của chiếc hộp theo \(x\).

c) Khảo sát hàm số \(S\left( x \right)\) trên khoảng \(\left( {0; + \infty } \right)\).

d) Tìm kích thước của hộp để tiết kiệm vật liệu nhất. (Làm tròn kết quả đến hàng đơn vị của mi-li-mét.)

Lời giải chi tiết

a) Thể tích của hình hộp là: \(V = xy.8 = 800 \Leftrightarrow y = \frac{{800}}{{8{\rm{x}}}} = \frac{{100}}{{\rm{x}}}\)

b) Diện tích toàn phần của hộp là:

\(S\left( x \right) = 2{\rm{x}}y + 2\left( {x + y} \right).8 = 2{\rm{x}}.\frac{{100}}{x} + 2\left( {x + \frac{{100}}{x}} \right).8 = 200 + 16{\rm{x}} + \frac{{1600}}{x}\)

c) Xét hàm số \(S\left( x \right) = 200 + 16{\rm{x}} + \frac{{1600}}{x}\) trên khoảng \(\left( {0; + \infty } \right)\).

1. Sự biến thiên:

• Chiều biến thiên:

Đạo hàm

\(S'\left( x \right) = 16 - \frac{{1600}}{{{x^2}}};S'\left( x \right) = 0 \Leftrightarrow x = 10\) hoặc \({\rm{x}} =  - 10\) (loại)

Trên khoảng \(\left( {10; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến trên khoảng đó.

Trên khoảng \(\left( {0;10} \right)\), \(y' < 0\) nên hàm số nghịch biến trên khoảng đó.

• Cực trị:

Hàm số đạt cực tiểu tại \(x = 10\) và \({y_{CT}} = 520\).

• Tiệm cận:

Ta có:  \(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} \left( {200 + 16{\rm{x}} + \frac{{1600}}{x}} \right) =  + \infty \)

Vậy \(x = 0\) là tiệm cận đứng của đồ thị hàm số đã cho.

Ta có:  \(a = \mathop {\lim }\limits_{x \to  + \infty } \frac{{f\left( x \right)}}{x} = \mathop {\lim }\limits_{x \to  + \infty } \left( {\frac{{16{{\rm{x}}^2} + 200x + 1600}}{{{x^2}}}} \right) = 16\) và

\(b = \mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - 16x} \right] = \mathop {\lim }\limits_{x \to  + \infty } \left[ {\left( {200 + 16{\rm{x}} + \frac{{1600}}{x}} \right) - 16x} \right] = \mathop {\lim }\limits_{x \to  + \infty } \left( {200 + \frac{{1600}}{x}} \right) = 200\)

Vậy đường thẳng \(y = 16{\rm{x}} + 200\) là tiệm cận xiên của đồ thị hàm số đã cho.

• Bảng biến thiên:

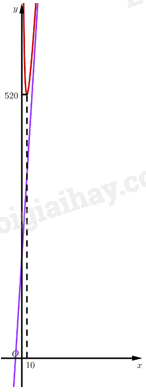
2. Đồ thị

Ta có \(y = 0 \Leftrightarrow 16{{\rm{x}}^2} + 200x + 1600 = 0\) (phương trình vô nghiệm).

Vậy đồ thị hàm số không có giao điểm với trục \(Ox\).

Đồ thị hàm số không có giao điểm với trục \(Oy\).

Vậy đồ thị hàm số được biểu diễn như hình vẽ bên.

d) Dựa vào đồ thị ta có \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} S\left( x \right) = S\left( {10} \right) = 520\).

Vậy để tiết kiệm vật liệu nhất thì \(x = 10\left( {cm} \right),y = \frac{{100}}{{10}} = 10\left( {cm} \right),h = 8\left( {cm} \right)\).