Bài 71 trang 113 SBT toán 9 tập 2

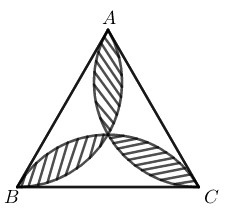
Đề bài

Trong một tam giác đều \(ABC\; (h.13),\) vẽ những cung tròn đi qua tâm của tam giác và từng cặp đỉnh của nó. Cho biết cạnh tam giác bằng \(a,\) tính diện tích hình hoa thị gạch sọc.

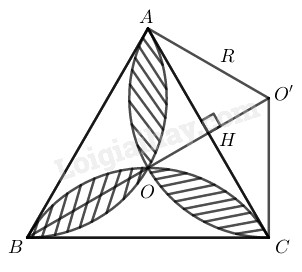
Lời giải chi tiết

Diện tích hình hoa thị bằng tổng diện tích \(3\) hình viên phân trừ diện tích tam giác đều \(ABC.\)

Gọi \(O\) là tâm của tam giác đều \(ABC\)

\( \Rightarrow OA = OB = OC\)

Vì \(∆ABC\) đều nên \(AO,\) \(BO,\) \(CO\) là phân giác của các góc \(\widehat A,\widehat B,\widehat C\)

\(\widehat {OAC} = \widehat {OCA} = \displaystyle {{{{60}^\circ}} \over 2} = {30^\circ}\)

\(\widehat {AOC} = {180^\circ} - \left( {{{30}^\circ} + {{30}^\circ}} \right) = {120^\circ}\)

Trong tam giác \(O’HA\) có \(\widehat {O'HA} = {90^\circ}\), \(\widehat {HO'A} = {60^\circ}\)

\(AH = R.\sin \widehat {HO'A}\)\( = R. \sin 60^\circ= \displaystyle {{R\sqrt 3 } \over 2}\)

\(AC=2AH=R\sqrt 3 \)

\( \Rightarrow R =\displaystyle  {\displaystyle {AC} \over {\sqrt 3 }} = {a \over {\sqrt 3 }} = {{a\sqrt 3 } \over 3}\)

\(S_{quạt}=\displaystyle {{\pi \displaystyle {{\left( {{\displaystyle {a\sqrt 3 } \over 3}} \right)}^2}.120} \over {360}}\)

     \(=\displaystyle {{\pi \displaystyle {{\displaystyle {a^2}} \over 3}} \over 3} = {{\pi {a^2}} \over 9}\) (đơn vị diện tích)

\(∆O'HA\) có \(\widehat {O'HA} = {90^\circ}\); \(\widehat {HO'A} = {60^\circ}\)

\(O'A=R.\cos {60^\circ} = \displaystyle {{a\sqrt 3 } \over 3}.{1 \over 2} = {{a\sqrt 3 } \over 6}\)

\(S_{\Delta O'CA}=\displaystyle {1 \over 2}O'H.AC \)\(\displaystyle = {1 \over 2}.{{a\sqrt 3 } \over 6}.a = {{{a^2}\sqrt 3 } \over {12}}\) (đơn vị diện tích)

Diện tích hình viên phân:

\(S_{vp}=S_{quạt}-S_{\Delta O'CA}\) \(= \displaystyle {{\pi {a^2}} \over 9} - {{{a^2}\sqrt 3 } \over {12}} = {{4\pi {a^2} - 3{a^2}\sqrt 3 } \over {36}}\)

Diện tích tam giác đều \(ABC\) cạnh \(a:\)  \(S_{ABC}= \dfrac{a^2\sqrt 3 } {4}\) (đơn vị diện tích)

Diện tích hình hoa thị là:

\(S=3S_{vp}-S_{ABC}\)\(= \displaystyle 3.{{4\pi {R^2} - 3{a^2}\sqrt 3 } \over {36}} - {{{a^2}\sqrt 3 } \over 4}\)

\(= \displaystyle {{4\pi {a^2} - 3{a^2}\sqrt 3 } \over {12}} - {{3{a^2}\sqrt 3 } \over {12}}\)

\(= \displaystyle {{4\pi {a^2} - 6{a^2}\sqrt 3 } \over {12}} = {{{a^2}} \over 6}\left( {2\pi  - 3\sqrt 3 } \right)\) (đơn vị diện tích)

Loigiaihay.com