Giải bài 7 trang 75 sách bài tập toán 10 - Chân trời sáng tạoa) Tính diện tích tam giác MNP b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP Quảng cáo
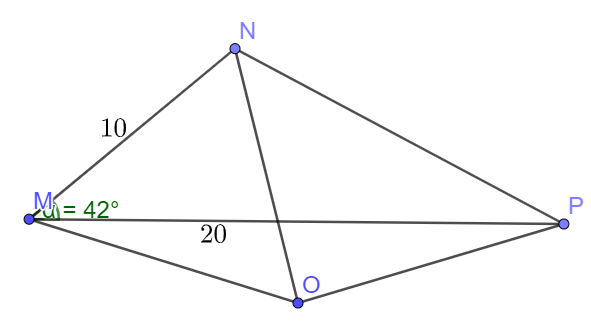
Đề bài Cho tam giác MNP có \(MN = 10,MP = 20\) và \(\widehat M = 42^\circ \) a) Tính diện tích tam giác MNP b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP Lời giải chi tiết
a) Ta có công thức \(S = \frac{1}{2}ab\sin C = \frac{1}{2}.MN.MP.\sin M\) \( = \frac{1}{2}.10.20.\sin 42^\circ \simeq 66,91\) (đvdt) b) O là tâm đường tròn ngoại tiếp tam giác MNP nên ta có: \(OM = ON = OP = R = \frac{{NP}}{{2\sin M}}\) (*) Áp dụng định lí côsin ta tính được NP như sau: \(NP = \sqrt {M{P^2} + M{N^2} - 2.MP.MN.\cos M} \simeq 14,24\) (cm) Thay NP vừa tính được vào (*) ta có: \(OM = ON = OP = R = \frac{{NP}}{{2\sin M}} = \frac{{14,24}}{{2.\sin 42^\circ }} \simeq 10,64\) Tam giác ONP có \(ON = OP = 10,64;NP = 14,24\) Áp dụng công thức Heron, ta có: \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \simeq 56,3\)(cm2)
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
