Giải bài 43 trang 74 sách bài tập toán 9 - Cánh diều tập 2Một biển báo giao thông có một phần dạng hình chữ thập với các kích thước x (cm), y (cm) và (y = x + 25,AL = AB = CD = DE = FG = GH = IJ = JK)như hình 13. a) Tính diện tích phần hình chữ thập của biển báo giao thông đó theo x. b) Tìm x nếu diện tích phần hình chữ thập của biển báo giao thông đó là 975cm2. Quảng cáo
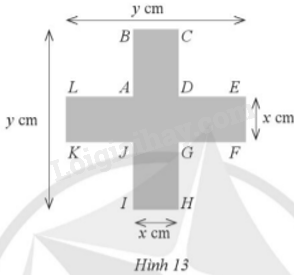
Đề bài Một biển báo giao thông có một phần dạng hình chữ thập với các kích thước x (cm), y (cm) và \(y = x + 25,\) \(AL = AB = CD = DE = FG = GH = IJ = JK\) như hình 13. a) Tính diện tích phần hình chữ thập của biển báo giao thông đó theo x. b) Tìm x nếu diện tích phần hình chữ thập của biển báo giao thông đó là 975cm2.
Phương pháp giải - Xem chi tiết a) Diện tích cần tìm = diện tích BCHI + diện tích LEFK - diện tích ADGJ b) Bước 1: Lập phương trình thể hiện diện tích phần hình chữ thập. Bước 2: Giải phương trình, đối chiếu điều kiện và kết luận. Lời giải chi tiết Điều kiện \(x > 0;y > 25\). a) Diện tích hình chữ nhật BCHI là \(xy = x\left( {x + 25} \right) = {x^2} + 25x\) (m2) Diện tích hình chữ nhật LEFK là \(xy = x\left( {x + 25} \right) = {x^2} + 25x\) (m2) Diện tích hình vuông ADGJ là \({x^2}\) (m2) Diện tích phần hình chữ thập là: \({x^2} + 25x + {x^2} + 25x - {x^2} = {x^2} + 50x\)(m2) b) Vì diện tích phần hình chữ thập của biển báo giao thông đó là 975cm2 nên ta có: \({x^2} + 50x = 975\), do đó \({x^2} + 50x - 975 = 0\) Ta có \(\Delta ' = {25^2} - 1.\left( { - 975} \right) = 1600 > 0\) nên phương trình có 2 nghiệm phân biệt: \({x_1} = \frac{{ - 25 - \sqrt {1600} }}{1} = - 65;{x_2} = \frac{{ - 25 + \sqrt {1600} }}{1} = 15\) Ta thấy \({x_1} = - 65\) không thỏa mãn điều kiện; \({x_2} = 15\) thỏa mãn điều kiện. Vậy \(x = 15\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
