Bài 43 trang 139 Vở bài tập toán 7 tập 1Giải bài 43 trang 139 VBT toán 7 tập 1. Cho tam giác ABC cân tại A( góc A<90^o)... Quảng cáo
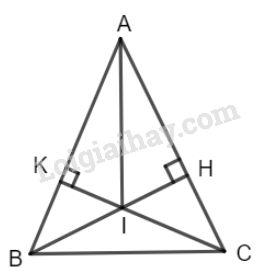
Đề bài Cho tam giác \( ABC\) cân tại \( A\) (\(\widehat{A}\)< \(90^o\)). Vẽ \(BH \perp A C\) (\( H\in AC\)), \(CK\perp AB\) (\( K \in AB\)) a) Chứng minh rằng \( AH = AK.\) b) Gọi \( I\) là giao điểm của \( BH\) và \( CK\). Chứng minh rằng tia \( AI \) là tia phân giác của góc \( A.\) Phương pháp giải - Xem chi tiết - Nếu canh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. - Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Lời giải chi tiết
a) Các tam giác vuông \(ABH \) và \( ACK\) có: \(AB = AC\) (vì tam giác \(ABC\) cân tại \(A\)) \(\widehat A\) chung Do đó \( \Delta ABH = \Delta ACK\) (cạnh huyền - góc nhọn). suy ra \( AH = AK\) (hai cạnh tương ứng). b) Các tam giác vuông \(AIH\) và \(AIK\) có: \(AH= AK \) (chứng minh trên) \(AI \) cạnh chung Do đó \( \Delta AIH= \Delta AIK \) (cạnh huyền- cạnh góc vuông) suy ra \( \widehat{IAK}=\widehat{IAH}\) (hai góc tương ứng) Vậy \(AI\) là tia phân giác của góc \(A\). Loigiaihay.com
|














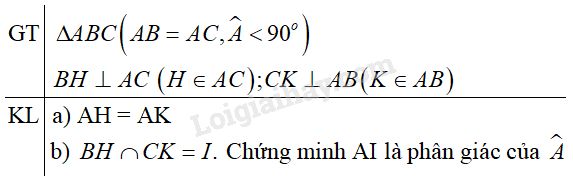






Danh sách bình luận