Giải bài 4.26 trang 61 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

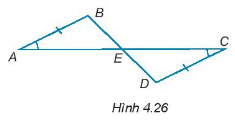
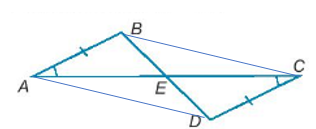
Đề bài

Cho các điểm A, B, C, D, E như Hình 4.26, biết rằng AB = CD, \(\widehat {BAE} = \widehat {DCE}\). Chứng minh rằng:

a) E là trung điểm của các đoạn thẳng AC và BD.

b) \(\Delta ACD = \Delta CAB\)

c) AD song song với BC. 

Lời giải chi tiết

a) Áp dụng định lí tổng ba góc trong tam giác ABE, ta có:

\(\widehat B +\widehat A + \widehat {AEB}=180^\circ\)

Áp dụng định lí tổng ba góc trong tam giác DCE, ta có:

\(\widehat D + \widehat C+ \widehat {DEC}=180^\circ\)

Mà \(\widehat {AEB} = \widehat {DEC}\) (2 góc đối đỉnh); \(\widehat{A}=\widehat{C}\)

nên \(\widehat B = \widehat D\)

Xét \(\Delta ABE\) và \(\Delta CDE\) có:

AB = CD (gt)

\(\widehat A = \widehat C\left( {gt} \right)\)

\(\widehat B = \widehat D\left( {cmt} \right)\)

Do đó \(\Delta ABE = \Delta CDE\left( {g - c - g} \right)\)

Suy ra AE = CE, BE = DE (cặp cạnh tương ứng)

Vậy E là trung điểm của các đoạn thẳng AC và BD.

b)

Xét \(\Delta ACD\) và \(\Delta CAB\) có:

AC: Cạnh chung

\(\widehat {ACD} = \widehat {CAB}\)(gt)

CD = AB (gt)

Vậy \(\Delta ACD = \Delta CAB\left( {c - g - c} \right)\)

c) Vì \(\Delta ACD = \Delta CAB\left( {cmt} \right) \) nên \( \widehat {CAD} = \widehat {ACB}\) (2 góc tương ứng)

Mà 2 góc ở vị trí so le trong

Do đó \(AD// BC\) (Dấu hiệu nhận biết 2 đường thẳng song song).