Giải bài 4.25 trang 61 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

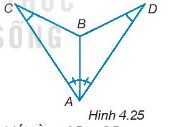
Đề bài

Cho các điểm A, B, C, D như Hình 4.25, biết rằng \(\widehat {BAC} = \widehat {BAD}\) và \(\widehat {BCA} = \widehat {BDA}\). Chứng minh rằng \(\Delta ABC = \Delta ABD\).

Lời giải chi tiết

Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:

\( \widehat {ABC}+\widehat {BAC} +\widehat {BCA}=180^\circ\)

Suy ra \(\widehat {ABC} = {180^\circ} - \widehat {BAC} - \widehat {BCA}\)

Áp dụng định lí tổng ba góc trong tam giác ABD, ta có:

\(\widehat {ABD} + \widehat {BAD} + \widehat {BDA}=180^\circ\)

suy ra \(\widehat {ABD} = {180^\circ} - \widehat {BAD} - \widehat {BDA}\)

Mà \(\widehat {BAC}=\widehat {BAD}; \widehat {BCA} = \widehat {BDA}\left( {gt} \right)\)

Do đó \(\widehat {ABC} = \widehat {ABD}\)

Xét \(\Delta ABC\) và \(\Delta ABD\) có:

\(\widehat {BAC} = \widehat {BAD}\left( {gt} \right)\)

AB chung

\( \widehat {ABC} = \widehat {ABD}\)

Vậy \(\Delta ABC = \Delta ABD\left( {g - c - g} \right)\)