Giải bài 36 trang 72 sách bài tập toán 9 - Cánh diều tập 2Cho biết đồ thị hàm số (y = left( {m + 2} right){x^2}left( {m ne - 2} right)) đi qua điểm (Aleft( { - 1; - 2} right)). a) Tính giá trị của hàm số tại (x = 3). b) Điểm (Bleft( {0,5; - 0,25} right)) có thuộc đồ thị hàm số hay không? c) Tìm một số điểm thuộc đồ thị hàm số (khác điểm O) rồi vẽ đồ thị hàm số đó. Quảng cáo
Đề bài Cho biết đồ thị hàm số \(y = \left( {m + 2} \right){x^2}\left( {m \ne - 2} \right)\) đi qua điểm \(A\left( { - 1; - 2} \right)\). a) Tính giá trị của hàm số tại \(x = 3\). b) Điểm \(B\left( {0,5; - 0,25} \right)\) có thuộc đồ thị hàm số hay không? c) Tìm một số điểm thuộc đồ thị hàm số (khác điểm O) rồi vẽ đồ thị hàm số đó. Phương pháp giải - Xem chi tiết Bước 1: Thay tọa độ điểm A vào hàm số để tìm m, từ đó được công thức cụ thể của hàm số. a) Bước 2: Thay \(x = 3\) vào hàm số vừa tìm được. b) Bước 3: Thay hoành độ của B vào vế phải của hàm số rồi so sánh với tung độ của B: nếu giá trị vừa tìm được bằng tung độ của B thì B thuộc đồ thị hàm số và ngược lại. c) Lấy giá trị x bất kì, từ đó tìm được y tương ứng (lấy ít nhất 4 giá trị). Lời giải chi tiết Đồ thị hàm số \(y = \left( {m + 2} \right){x^2}\left( {m \ne - 2} \right)\) đi qua điểm \(A\left( { - 1; - 2} \right)\) nên ta có: \( - 2 = \left( {m + 2} \right){\left( { - 1} \right)^2}\) hay \( - 2 = m + 2\), suy ra \(m = - 4\) (thỏa mãn điều kiện). Vậy hàm số có dạng \(y = \left( { - 4 + 2} \right){x^2}\) hay \(y = - 2{x^2}\) a) Tại \(x = 3\), ta có \(y = - 2{x^2} = - {2.3^2} = - 18\). Vậy \(x = 3\) thì hàm số có giá trị là \( - 18\). b) Xét \(B\left( {0,5; - 0,25} \right)\): Với \(x = 0,5\) thì \( - 2{x^2} = - {2.0,5^2} = - 0,5 \ne 0,5\). Vậy \(B\left( {0,5; - 0,25} \right)\) không thuộc đồ thị hàm số. c) Bảng giá trị:
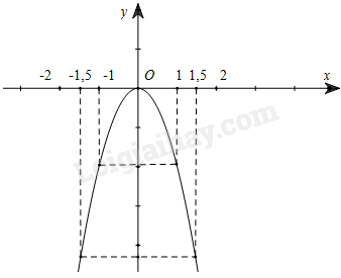
Đồ thị hàm số \(y = - 2{x^2}\) là đường parabol đi qua 5 điểm \(\left( { - 1,5; - 4,5} \right);\left( { - 1; - 2} \right);\left( {0;0} \right);\left( {1; - 2} \right);\left( {1,5; - 4,5} \right)\)
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
