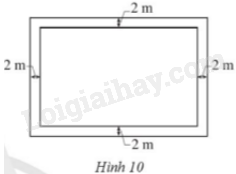
Giải bài 33 trang 72 sách bài tập toán 9 - Cánh diều tập 2Một mảnh đất hình chữ nhật có chiều rộng x (m), chiều dài gấp rưỡi chiều rộng. Người ta đã làm một vườn hoa ở trung tâm mảnh đất với diện tích bằng 640 m và làm một con đường rộng 2 m xung quanh vườn hoa đó (Hình 10). Hỏi chu vi của mảnh đất đó bằng bao nhiêu mét? Quảng cáo
Đề bài Một mảnh đất hình chữ nhật có chiều rộng x (m), chiều dài gấp rưỡi chiều rộng. Người ta đã làm một vườn hoa ở trung tâm mảnh đất với diện tích bằng 640 m và làm một con đường rộng 2 m xung quanh vườn hoa đó (Hình 10). Hỏi chu vi của mảnh đất đó bằng bao nhiêu mét?
Phương pháp giải - Xem chi tiết Bước 1: Biểu diễn chiều dài mảnh đất theo x. Bước 2: Biểu diễn chiều dài, chiều rộng vườn hoa theo x. Bước 3: Dựa vào diện tích vườn hoa để lập phương trình. Bước 4: Giải phương trình, loại giá trị x không phù hợp. Bước 5: Tìm chiều dài rồi tính chu vi mảnh đất. Lời giải chi tiết Chiều dài mảnh đất là \(1,5x\)(m), điều kiện \(x > 0\). Chiều dài và chiều rộng vườn hoa lần lượt là: \(1,5x - 4\) và \(x - 4\) (m). Vườn hoa có diện tích là 640m nên ta có \(\left( {1,5x - 4} \right)\left( {x - 4} \right) = 640\) hay \(1,5{x^2} - 10x - 624 = 0\) Ta có \(\Delta ' = {\left( { - 5} \right)^2} - 1,5.\left( { - 624} \right) = 961 > 0\). Do \(\Delta ' > 0\) nên phương trình có 2 nghiệm phân biệt \(x = \frac{{ - \left( { - 5} \right) - \sqrt {961} }}{{1,5}} = \frac{{ - 52}}{3};x = \frac{{ - \left( { - 5} \right) + \sqrt {961} }}{{1,5}} = 24\) Ta thấy \(x = 24\) thỏa mãn điều kiện nên chiều rộng mảnh đất là 24m. Chiều dài mảnh đất là \(1,5x = 1,5.24 = 36\)m. Chu vi mảnh đất là: \(2\left( {24 + 36} \right) = 120\)m.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
