Giải bài 3 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1Cho biết (soversetfrown{AB}=soversetfrown{BC}=soversetfrown{CA}) và OB = R. Độ dài cạnh BC là: A. (Rsqrt 3 ) B. (frac{{Rsqrt 3 }}{2}) C. (Rsqrt 2 ) D. (frac{{Rsqrt 3 }}{3}) Quảng cáo
Đề bài Cho biết \(sđ\overset\frown{AB}=sđ\overset\frown{BC}=sđ\overset\frown{CA}\) và OB = R. Độ dài cạnh BC là: A. \(R\sqrt 3 \) B. \(\frac{{R\sqrt 3 }}{2}\) C. \(R\sqrt 2 \) D. \(\frac{{R\sqrt 3 }}{3}\)
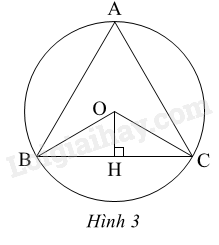
Phương pháp giải - Xem chi tiết Dựa vào: Góc ở tâm bằng số đo cung cùng chắn một cung. Lời giải chi tiết Ta có \(sđ\overset\frown{AB}=sđ\overset\frown{BC}=sđ\overset\frown{CA}=\frac{{{360}^{o}}}{3}={{120}^{o}}\) suy ra \(\widehat {BOC} = {120^o}\) (góc ở tâm bằng số đo cung cùng chắn một cung). Mặt khác \(\Delta BOH = \Delta COH(g.c.g)\) suy ra \(\widehat {BOH} = \widehat {COH} = \frac{{\widehat {BOC}}}{2} = \frac{{{{120}^o}}}{2} = {60^o}.\) Xét tam giác vuông BOH, ta có: BH = sin\(\widehat {BOH}\). R = sin 60o .R = \(\frac{{\sqrt 3 R}}{2}\) Vậy BC = BH + HC = 2BH = 2. \(\frac{{\sqrt 3 R}}{2}\)= \(R\sqrt 3 \). Chọn đáp án A.
|




















Danh sách bình luận