Giải bài 3 trang 72 sách bài tập toán 9 - Chân trời sáng tạo tập 1

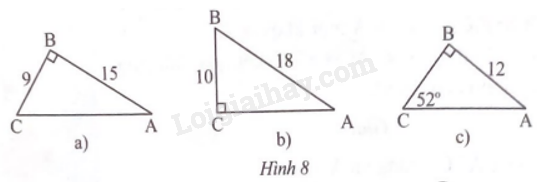
Đề bài

Giải tam giác vuông ABC trong mỗi trường hợp sau:

 

Lời giải chi tiết

a) \(AC = \sqrt {B{A^2} + B{C^2}}  = \sqrt {{{15}^2} + {9^2}}  \approx 17,49\)

tan \(A = \frac{{BC}}{{BA}} = \frac{9}{{15}} = 0,6\)

suy ra \(\widehat A \approx {30^o}58'\); \(\tan C = \frac{{BA}}{{BC}} = \frac{{15}}{9} = \frac{5}{3}\), suy ra \(\widehat C \approx {59^o}2'\).

b) \(AC = \sqrt {A{B^2} - B{C^2}}  = \sqrt {{{18}^2} - {{10}^2}}  \approx 14,97\)

sin \(A = \frac{{BC}}{{AB}} = \frac{{10}}{{18}} = \frac{5}{9}\);

suy ra \(\widehat A \approx {33^o}45'\); \(\cos B = \frac{{BC}}{{AB}} = \frac{{10}}{{18}} = \frac{5}{9}\), suy ra \(\widehat B \approx {56^o}15'\).

c) \(\widehat A = 90 - \widehat C = {90^o} - {52^o} = {38^o}\); \(BC = AB\tan A = 12.\tan {38^o} \approx 9,38\).

\(AC = \frac{{AB}}{{\sin C}} = \frac{{12}}{{\sin {{52}^o}}} \approx 15,23.\)