Bài 2.9 trang 104 SBT giải tích 12Giải bài 2.9 trang 104 sách bài tập giải tích 12. Vẽ đồ thị của hai hàm số sau trên cùng một hệ trục tọa độ:... Quảng cáo
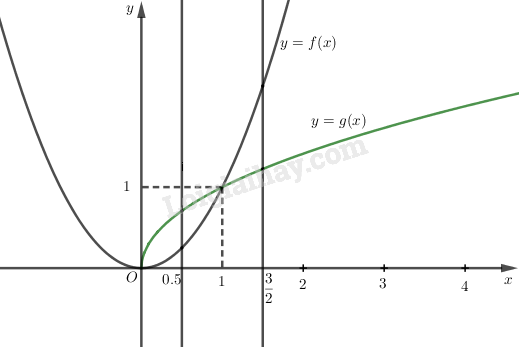
Đề bài Vẽ đồ thị của các hàm số \(y = {x^2}\) và \(y = {x^{\frac{1}{2}}}\) trên cùng một hệ trục tọa độ. Hãy so sánh giá trị của các hàm số đó khi \(x = 0,5;1;\dfrac{3}{2};2;3;4.\) Phương pháp giải - Xem chi tiết - Vẽ đồ thị các hàm số đã cho dựa vào kiến thức đã học về hàm số bậc hai và hàm số lũy thừa. - So sánh giá trị của hai hàm số tại các điểm \(x = {x_i}\) bằng cách dựng đường thẳng \(x = {x_i}\) và nhận xét vị trí các điểm giao trên hình vẽ. Quảng cáo  Lời giải chi tiết Đặt \(f(x) = {x^2},x \in R\);\(g(x) = {x^{\frac{1}{2}}},x > 0\) Vẽ đồ thị hai hàm số ta được:
Từ đồ thị của hai hàm số ta thấy: +) \(f(0,5) < g(0,5)\); +) \(f(1) = g(1) = 1\); +) \(f\left( {\dfrac{3}{2}} \right) > g\left( {\dfrac{3}{2}} \right)\); +) \(f(2) > g(2)\); +) \(f(3) > g(3)\); +) \(f(4) > g(4)\). Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
|
