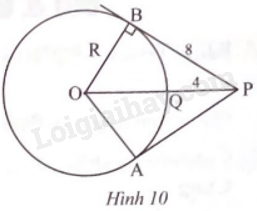
Giải bài 2 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 1Từ điểm P ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Đoạn thẳng OP cắt (O) tại Q (Hình 10). Cho biết PB = 8, PQ = 4. Tính R và số đo (widehat {AOB}). Quảng cáo
Đề bài Từ điểm P ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Đoạn thẳng OP cắt (O) tại Q (Hình 10). Cho biết PB = 8, PQ = 4. Tính R và số đo \(\widehat {AOB}\).
Phương pháp giải - Xem chi tiết Áp dụng định lí Pythagore vào tam giác OPB để tính R. Sử dụng tỉ số lượng giác, từ đó tính góc BOP. Khi đó ta tính được góc AOB. Lời giải chi tiết Trong \(\Delta OPB\) vuông tại B, ta có OP2 = OB2 + PB2, suy ra (R + 4)2 = R2 + 82, suy ra R = 6. OP2 = OB2 + PB2 suy ra (R + 4)2 = R2 + 82, suy ra R = 6. \(\sin \widehat {BOP} = \frac{{PB}}{{OP}} = \frac{8}{{6 + 4}} = \frac{4}{5}\) suy ra \(\widehat {BOP} \approx {53^o}\). Ta lại có \(\widehat {AOB} = 2\widehat {BOP} \approx {2.53^o} = {106^o}.\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
