Giải bài 18 trang 101 sách bài tập toán 9 - Chân trời sáng tạo tập 1

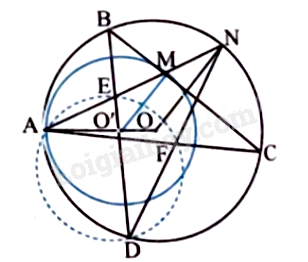
Đề bài

Cho hai đường tròn (O; R) và (O’; R’) (R > R’) tiếp xúc trong tại A. Một tiếp tuyến của đường tròn (O’) tại M cắt đường tròn (O) tại hai điểm B, C. Đường thẳng BO’ cắt đường tròn (O) tại điểm thứ hai D và cắt đường thẳng AM tại E. Gọi F là giao điểm thứ hai của đường tròn ngoại tiếp tam giác ADE với AC và N là giao điểm thứ hai của AN với (O). Chứng minh rằng:

a) O’M // ON.

b) Ba điểm D, N, F thẳng hàng.

c) DF là tia phân giác của góc \(\widehat {BDC}\).

Lời giải chi tiết

a) Ta có \(\widehat {AMO'} = \widehat {O'AM} = \widehat {OAN} = \widehat {ANO},\) suy ra O’M // ON.

b) Do O’M \( \bot \) BC nên ta cũng có ON \( \bot \) BC hay N là điểm chính giữa cung \(\overset\frown{BC}\).

Mặt khác \(\widehat{NAC}=\widehat{NDC}=\frac{1}{2}sđ\overset\frown{NC}\), \(\widehat{BDN}=\frac{1}{2}sđ\overset\frown{BN}\) nên \(\widehat {BDN} = \widehat {NAC} = \widehat {EAF}\). (1)

Trong đường tròn ngoại tiếp tam giác ADE, ta có \(\widehat {EAF} = \widehat {EDF} = \widehat {BDF}\)  (2)

Từ (1) và (2), ta có \(\widehat {BDF} = \widehat {BDN}\), suy ra D, N, F thẳng hàng.

c) Ta có hai cung \(\overset\frown{BN}\) và \(\overset\frown{NC}\) có số đo bằng nhau, suy ra \(\widehat {BDN} = \widehat {NDC}\) hay DF là tia phân giác của \(\widehat {BDC}\).