Bài 1.17 trang 15 SBT giải tích 12

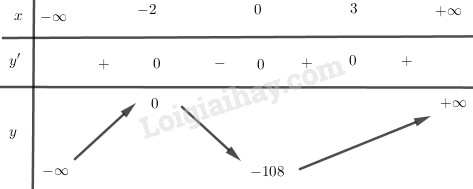
LG a

\(y =  - 2{x^2} + 7x - 5\).

Phương pháp giải:

- Tính \( y'\).

- Tính \(y''\).

- Tính giá trị của \(y''\) tại các điểm làm cho \(y'=0\) và kết luận.

+ Các điểm làm cho \(y''<0\) thì đó là điểm cực đại.

+ Các điểm làm cho \(y''>0\) thì đó là điểm cực tiểu.

Lời giải chi tiết:

TXĐ: R

\(\eqalign{
& y' = - 4x + 7\cr &y' = 0  \Leftrightarrow  - 4x + 7 = 0 \Leftrightarrow x = {7 \over 4} \cr 
& y'' = - 4  \Rightarrow  y''({7 \over 4}) = - 4 < 0 \cr} \)

Vậy \(x = {7 \over 4}\) là điểm cực đại của hàm số

\({y_{CD}} =  - 2.{\left( {\frac{7}{4}} \right)^2} + 7.\frac{7}{4} - 5 = \frac{9}{8}\)

LG b

\(y = {x^3} - 3{x^2} - 24x + 7\)

Phương pháp giải:

- Tính \( y'\).

- Tính \(y''\).

- Tính giá trị của \(y''\) tại các điểm làm cho \(y'=0\) và kết luận.

+ Các điểm làm cho \(y''<0\) thì đó là điểm cực đại.

+ Các điểm làm cho \(y''>0\) thì đó là điểm cực tiểu.

Lời giải chi tiết:

TXĐ: R

\(y' = 3{x^2} - 6x - 24 = 3({x^2} - 2x - 8)\)

\(y' = 0  \Leftrightarrow {x^2} - 2x - 8 = 0\) \(\Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr 
x = 4 \hfill \cr} \right.\)

\(y'' = 6x - 6\)

Vì \(y''( - 2) = 6.(-2)-6= - 18 < 0\) nên hàm số đạt cực đại tại \(x = - 2\) và y_CĐ = y(-2) = 35.

\(y''(4) =6.4-6= 18 > 0\) nên hàm số đạt cực tiểu tại \( x = 4 \) và y_CT = y(4) = -73.

LG c

\(y = {(x + 2)^2}{(x - 3)^3}\)

Phương pháp giải:

- Tính \( y'\).

- Lập bảng biến thiên và kết luận.

Lời giải chi tiết:

TXĐ: R

\(y' = 2(x + 2){(x - 3)^3} + 3{(x + 2)^2}{(x - 3)^2} \)

\(= \left( {x + 2} \right){\left( {x - 3} \right)^2}\left[ {2\left( {x - 3} \right) + 3\left( {x + 2} \right)} \right] \) \(= \left( {x + 2} \right){\left( {x - 3} \right)^2}\left( {2x - 6 + 3x + 6} \right)\)

\(= 5x(x + 2){(x - 3)^2}\)

\(y' = 0 \Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr 
x = 0 \hfill \cr 
x = 3 \hfill \cr} \right.\) 

Bảng biến thiên:

Từ đó suy ra y_CĐ = y(-2) = 0 ; y_CT = y(0) = -108.

Loigiaihay.com