Giải bài 1.10 trang 10 sách bài tập toán 12 - Kết nối tri thức

Đề bài

Một vật chuyển động dọc theo một trục số nằm ngang, chiều dương từ trái sang phải. Giả sử vị trí của vật \(x\) (mét) từ thời điểm \(t = 0\) giây đến thời điểm \(t = 5\) giây được cho bởi công thức \(x\left( t \right)={{t}^{3}}-7{{t}^{2}}+11t+5\).

a) Xác định vận tốc \(v\) của vật. Xác định khoảng thời gian vật chuyển động sang phải và khoảng thời gian vật chuyển động sang trái.

b) Tìm tốc độ của vật và thời điểm vật dừng lại. Tính tốc độ cực đại của vật trong khoảng thời gian từ \(t = 1\) đến \(t = 4\) giây.

c) Xác định gia tốc \(a\) của vật. Tìm khoảng thời gian vật tăng tốc và khoảng thời gian vật giảm tốc.

Lời giải chi tiết

Ta có \(x\left( t \right) = {t^3} - 7{t^2} + 11t + 5,t \in \left[ {0;5} \right]\).

a) Vận tốc của vật là \(v\left( t \right) = x'\left( t \right) = 3{t^2} - 14t + 11,t \in \left[ {0;5} \right]\) (m/s).

Ta có \(v\left( t \right) = 0 \Leftrightarrow 3{t^2} - 14t + 11 = 0 \Leftrightarrow t = 1\) hoặc \(t = \frac{{11}}{3}\).

Theo đề bài, vật chuyển động với chiều dương từ trái sang phải tức là vật chuyển động sang phải khi \(v\left( t \right) > 0\) và chuyển động sang trái khi \(v\left( t \right) < 0\).

Ta xét dấu của \(v\left( t \right)\) trên \(\left[ {0;5} \right]\):

Ta có \(v\left( t \right) > 0\) khi \(t \in \left( {0;1} \right)\) hoặc \(t \in \left( {\frac{{11}}{3};5} \right)\); \(v\left( t \right) < 0\) khi  \(t \in \left( {1;\frac{{11}}{3}} \right)\).

Do đó vật chuyển động sang phải trong khoảng thời điểm từ \(0\) giây đến \(1\) giây và từ \(\frac{{11}}{3}\) giây đến \(5\) giây; vật chuyển động sang trái trong khoảng thời điểm từ \(1\) giây đến \(\frac{{11}}{3}\) giây.

b) Tốc độ của vật là \(\left| {v\left( t \right)} \right| = x'\left( t \right) = 3{t^2} - 14t + 11,t \in \left[ {0;5} \right].\)

Vật dừng lại khi tốc độ bằng \(0\). Ta có \(\left| {v\left( t \right)} \right| = 0 \Leftrightarrow 3{t^2} - 14t + 11 = 0 \Leftrightarrow t = 1\) hoặc \(t = \frac{{11}}{3}\).

Suy ra vật dừng lại tại thời điểm \(t = 1\) giây hoặc \(t = \frac{{11}}{3}\) giây.

Xét \(v\left( t \right) = 3{t^2} - 14t + 11,t \in \left[ {1;4} \right]\). Tốc độ cực đại của vật từ \(t = 1\) giây đến \(t = 4\) giây là \(\mathop {\max }\limits_{t \in \left[ {1;4} \right]} \left| {v\left( t \right)} \right|\).

Xét hàm số \(\left| {v\left( t \right)} \right| = \left| {3{t^2} - 14t + 11} \right|,t \in \left[ {1;4} \right]\)

Ở ý a ta đã xét dấu của \(v\left( t \right)\) trên \(\left[ {0;5} \right]\) nên ta thu được dấu \(v\left( t \right)\) trên \(\left[ {1;4} \right]\) như sau: \(v\left( t \right) > 0\) khi \(t \in \left( {\frac{{11}}{3};4} \right)\); \(v\left( t \right) < 0\) khi  \(t \in \left( {1;\frac{{11}}{3}} \right)\).

Do đó ta có giá trị của hàm \(\left| {v\left( t \right)} \right|\) trên \(\left[ {1;4} \right]\) là

+ \(\left| {v\left( t \right)} \right| = v\left( t \right) = 3{t^2} - 14t + 11,t \in \left( {\frac{{11}}{3};4} \right)\)

+ \(\left| {v\left( t \right)} \right| =  - v\left( t \right) =  - 3{t^2} + 14t - 11,t \in \left( {1;\frac{{11}}{3}} \right)\)

Lập bảng xét dấu \(\left| {v\left( t \right)} \right|\) trên \(\left[ {1;4} \right]\) như sau

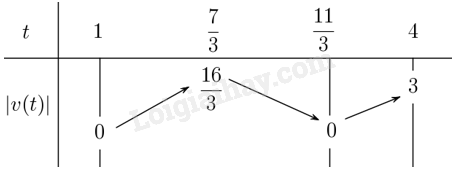
Từ bảng trên ta có \(\mathop {\max }\limits_{t \in \left[ {1;4} \right]} \left| {v\left( t \right)} \right| = \frac{{16}}{3}\).

Vậy tốc độ cực đại của vật từ \(t = 1\) giây đến \(t = 4\) giây là \(\frac{{16}}{3}\) m/s.

c) Gia tốc của vật là \(a\left( t \right) = v'\left( t \right) = 6t - 14\). Khi đó \(a\left( t \right) = 0 \Leftrightarrow 6t - 14 = 0 \Leftrightarrow t = \frac{7}{3}\)

Vật tăng tốc khi \(\) và giảm tốc khi \(a\left( t \right) < 0\). Với \(t \in \left[ {0;5} \right]\) ta có:

\(a\left( t \right) > 0\) khi \(t \in \left[ {\frac{7}{3};5} \right]\) và \(a\left( t \right) < 0\) khi \(t \in \left[ {0;\frac{7}{3}} \right]\).

Vậy vật tăng tốc trong khoảng thời gian từ \(\frac{7}{3}\) giây đến \(5\) giây và giảm tốc trong khoảng thời gian từ \(0\) giây đến \(\frac{7}{3}\) giây.