Giải bài 11 trang 11 sách bài tập toán 12 - Chân trời sáng tạoĐộ cao (tính bằng mét) của tàu lượn siêu tốc so với mặt đất sau \(t\)(giây) \(\left( {0 \le t \le 20} \right)\) từ lúc bắt đầu được cho bởi công thức \(h\left( t \right) = - \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} - \frac{{98}}{{17}}t + 20\). Trong khoảng thời gian nào tàu lượn đi xuống, trong khoảng thời gian nào tàu lượn đi lên? Quảng cáo
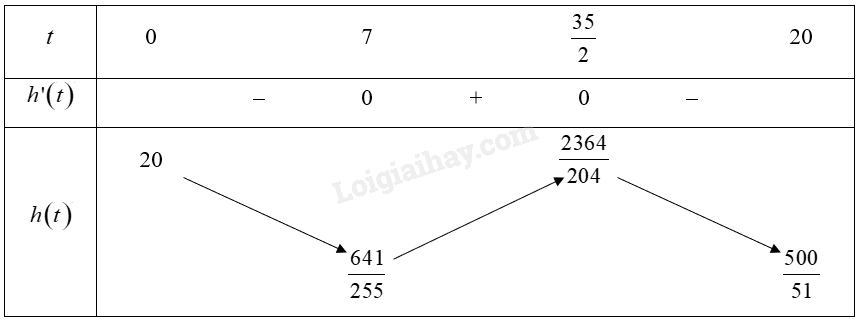
Đề bài Độ cao (tính bằng mét) của tàu lượn siêu tốc so với mặt đất sau \(t\)(giây) \(\left( {0 \le t \le 20} \right)\) từ lúc bắt đầu được cho bởi công thức \(h\left( t \right) = - \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} - \frac{{98}}{{17}}t + 20\). Trong khoảng thời gian nào tàu lượn đi xuống, trong khoảng thời gian nào tàu lượn đi lên? Phương pháp giải - Xem chi tiết Xét hàm số \(h\left( t \right)\) trên đoạn \(\left[ {0;20} \right]\), lập bảng biến thiên và tìm khoảng đồng biến, nghịch biến của hàm số. Lời giải chi tiết Xét hàm số \(h\left( t \right) = - \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} - \frac{{98}}{{17}}t + 20\) trên đoạn \(\left[ {0;20} \right]\). Ta có: \(h'\left( t \right) = - \frac{4}{{85}}{t^2} + \frac{{98}}{{85}}t - \frac{{98}}{{17}};h'\left( t \right) = 0 \Leftrightarrow t = \frac{{35}}{2}\) hoặc \(t = 7\). Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng \(\left( {7;\frac{{35}}{2}} \right)\), hàm số nghịch biến trên các khoảng \(\left( {0;7} \right)\) và \(\left( {\frac{{35}}{2};20} \right)\). Vậy tàu lượn đi lên trong khoảng thời gian từ 7 giây đến 17,5 giây, tàu lượn đi xuống trong khoảng thời gian từ 0 giây đến 7 giây và từ 17,5 giây đến 20 giây.
|




















Danh sách bình luận