Giải bài 1 trang 16 sách bài tập toán 12 - Chân trời sáng tạoTìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 2. Quảng cáo
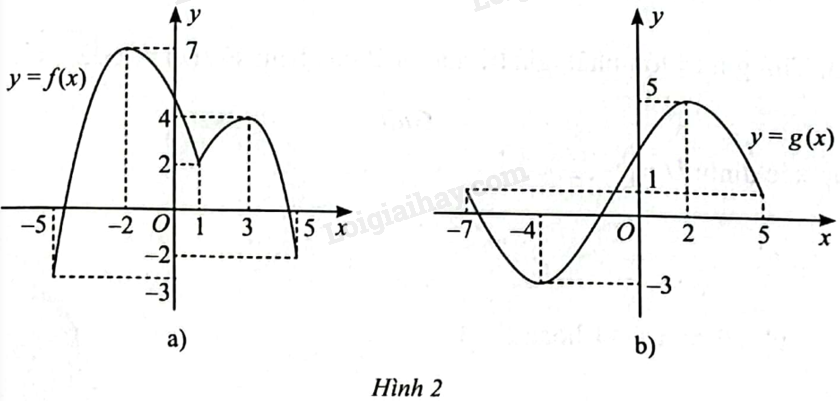
Đề bài Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 2.
Phương pháp giải - Xem chi tiết Dựa vào đồ thị hàm số. Lời giải chi tiết Dựa vào đồ thị ta có: a) \(\mathop {\max }\limits_{\left[ { - 5;5} \right]} f\left( x \right) = f\left( { - 2} \right) = 7,\mathop {\min }\limits_{\left[ { - 5;5} \right]} f\left( x \right) = f\left( { - 5} \right) = - 3\); b) \(\mathop {\max }\limits_{\left[ { - 7;5} \right]} g\left( x \right) = g\left( 2 \right) = 5,\mathop {\min }\limits_{\left[ { - 7;5} \right]} g\left( x \right) = g\left( { - 4} \right) = - 3\).
|




















Danh sách bình luận