Đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 9Phần trắc nghiệm (3 điểm) Câu 1: Trong các dữ liệu sau, dữ liệu nào là số liệu?Đề bài
I. Trắc nghiệm
Câu 1 :
Trong các dữ liệu sau, dữ liệu nào là số liệu?
Câu 2 :
Dữ liệu nào không hợp lí trong các dãy dữ liệu sau: Thủ đô của một số quốc gia Châu Á:
Câu 3 :
Để chuẩn bị cho đợt tham quan sắp tới của lớp, Nam đã tìm kiếm một số địa điểm du lịch ở Hà Nội trên Facebook, Zalo, Instagram, Google,…. để các bạn lựa chọn. Nam đã thu thập dữ liệu bằng cách:
Câu 5 :
Bộ ba độ dài đoạn thẳng nào sau đây tạo thành một tam giác?
Câu 8 :
Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
Câu 9 :
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
Câu 10 :
Biến cố “Ngày mai có mưa rào và dông ở Nam Định” là
Câu 11 :
Khi bắt đầu trận đấu bóng đá, trọng tài cho hai đội trưởng của hai đội bốc thăm để xem đội nào giao bóng trước. Xác suất để mỗi đội được giao bóng trước là
Câu 12 :
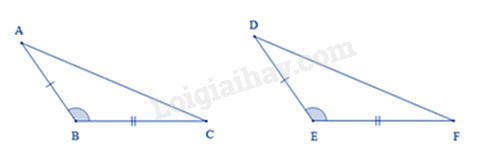
Hai tam giác bằng nhau là
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Trong các dữ liệu sau, dữ liệu nào là số liệu?
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về phân loại dữ liệu. Lời giải chi tiết :
Dữ liệu Số học sinh đi học muộn trong một buổi học là số liệu.
Câu 2 :
Dữ liệu nào không hợp lí trong các dãy dữ liệu sau: Thủ đô của một số quốc gia Châu Á:
Đáp án : A Phương pháp giải :
Xác định dữ liệu không hợp lí. Lời giải chi tiết :
Dữ liệu không hợp lí là Hồ Chí Minh vì thành phố Hồ Chí Minh không phải thủ đô của quốc gia.
Câu 3 :
Để chuẩn bị cho đợt tham quan sắp tới của lớp, Nam đã tìm kiếm một số địa điểm du lịch ở Hà Nội trên Facebook, Zalo, Instagram, Google,…. để các bạn lựa chọn. Nam đã thu thập dữ liệu bằng cách:
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về thu thập dữ liệu. Lời giải chi tiết :
Nam đã thu thập dữ liệu bằng cách thu thập từ trang web.
Đáp án : D Phương pháp giải :
Quan sát biểu đồ để xác định. Lời giải chi tiết :
GDP Việt Nam năm 2019 là 261 tỉ USD.
Câu 5 :
Bộ ba độ dài đoạn thẳng nào sau đây tạo thành một tam giác?
Đáp án : B Phương pháp giải :
Dựa vào quan hệ giữa ba cạnh của một tam giác. Lời giải chi tiết :
Ta có: 5 – 4 = 1 nên 5cm; 4cm; 1cm không thể tạo thành một tam giác. 3cm; 4cm; 5cm có thể tạo thành một tam giác nên ta chọn đáp án B. 2 + 2 = 4 < 5 nên 5cm; 2cm; 2cm không thể tạo thành một tam giác. 1 + 4 = 5 < 10 nên 1cm; 4cm; 10cm không thể tạo thành một tam giác.
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về hai tam giác bằng nhau. Lời giải chi tiết :
Xét tam giác ABC và tam giác DEF có: \(\begin{array}{l}AB = DE\\\widehat {ABC} = \widehat {DEF}\\BC = EF\end{array}\) Suy ra \(\Delta ABC = \Delta DEF\) (cạnh – góc – cạnh)
Đáp án : D Phương pháp giải :
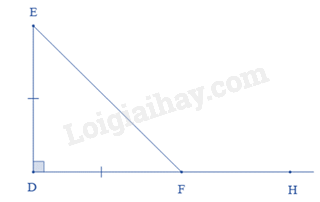
Dựa vào tính chất của tam giác cân và hai góc kề bù. Lời giải chi tiết :
Tam giác DEF có \(\widehat D = {90^0}\) và DE = DF nên tam giác DEF vuông cân tại D. Suy ra \(\widehat {DEF} = \widehat {DFE} = \frac{{{{180}^0} - {{90}^0}}}{2} = {45^0}\). Ta có \(\widehat {DFE} + \widehat {EFH} = {180^0}\) (hai góc kề bù) Suy ra \(\widehat {EFH} = {180^0} - \widehat {DFE} = {180^0} - {45^0} = {135^0}\).
Câu 8 :
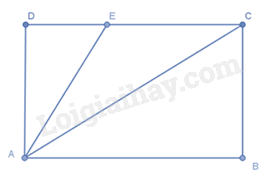
Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
Đáp án : A Phương pháp giải :
Dựa vào quan hệ giữa đường xiên và hình chiếu. Lời giải chi tiết :
Xét tam giác vuông ACD có AD < AC (trong tam giác vuông, cạnh huyền là cạnh lớn nhất) Vì E nằm trên cạnh CD nên DE < DC suy ra AE < AC (quan hệ giữa đường vuông góc và đường xiên. Suy ra AD < AE < AC nên A sai.
Câu 9 :
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
Đáp án : D Phương pháp giải :
Dựa vào khái niệm về đường trung trực của đoạn thẳng. Lời giải chi tiết :
“Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó”.
Câu 10 :
Biến cố “Ngày mai có mưa rào và dông ở Nam Định” là
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về biến cố. Lời giải chi tiết :
Biến cố “Ngày mai có mưa rào và dông ở Nam Định” là biến cố ngẫu nhiên vì điều này không chắc có thể xảy ra.
Câu 11 :
Khi bắt đầu trận đấu bóng đá, trọng tài cho hai đội trưởng của hai đội bốc thăm để xem đội nào giao bóng trước. Xác suất để mỗi đội được giao bóng trước là
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về xác suất của biến cố. Lời giải chi tiết :
Vì có hai đội nên xác suất để mỗi đội được giao bóng trước là 50%.
Câu 12 :
Hai tam giác bằng nhau là
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về hai tam giác bằng nhau. Lời giải chi tiết :
Hai tam giác bằng nhau là hai tam giác có ba cặp cạnh, ba cặp góc tương ứng bằng nhau.
II. Tự luận
Phương pháp giải :
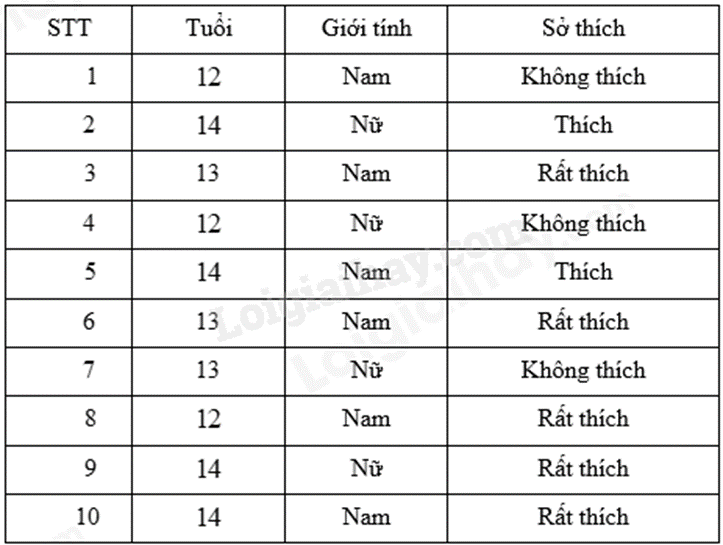
Quan sát bảng thống kê để trả lời câu hỏi. Lời giải chi tiết :
a) Các mức độ thể hiện sự yêu thích đối với môn bóng đá của các học sinh được điều tra là: Không thích, Thích, Rất thích. b) Có \(6\) học sinh nam, \(4\) học sinh nữ được điều tra. c) Độ tuổi trung bình của các học sinh được điều tra là: \(\frac{{12 + 14 + 13 + 12 + 14 + 13 + 13 + 12 + 14 + 14}}{{10}} = 13,1\) (tuổi) Phương pháp giải :
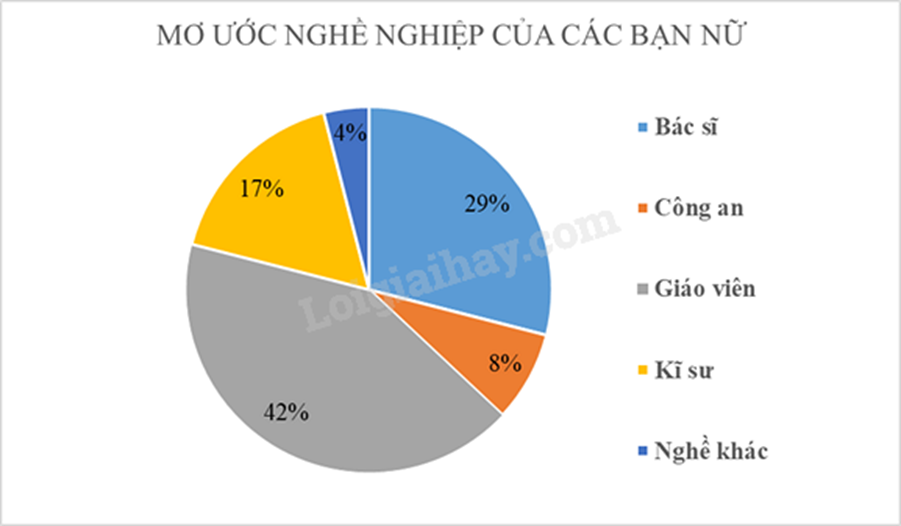
Quan sát biểu đồ để trả lời câu hỏi. Lời giải chi tiết :
a) Nghề nghiệp được các bạn nữ yêu thích nhất là Giáo viên (với 42% bạn nữ chọn). b) Số học sinh nữ của khối 7 là: \(16:8\% = 200\) (bạn) Phương pháp giải :
Xác định các kết quả có thể, các kết quả thuận lợi cho biến cố. Xác suất của biến cố bằng tỉ số của số kết quả thuận lợi của biến cố với tổng số kết quả. Lời giải chi tiết :
Có 6 kết quả có thể khi gieo ngẫu nhiên một con xúc xắc 1 lần đó là: 1; 2; 3; 4; 5; 6. * Có 1 kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số số 2” là 2. Xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số 2” là \(\frac{1}{6}\). * Có 3 kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” là 2; 4; 6. Xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” là \(\frac{3}{6}\). * Có 2 kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 1” là 1; 4. Xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 1” là \(\frac{2}{6} = \frac{1}{3}\). Phương pháp giải :
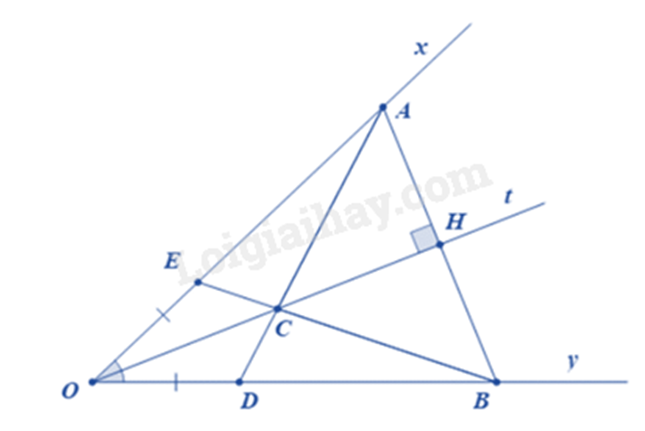
a) Chứng minh được: ∆AHO = ∆BHO (góc – cạnh – góc) Suy ra OA = OB (hai cạnh tương ứng) b) Chứng minh được: ∆AHC = ∆BHC (hai cạnh góc vuông) Suy ra \(\widehat {ACH} = \widehat {HCB}\) (hai góc tương ứng) c) Chứng minh được: ∆OEC = ∆ODC (c.g.c) Chứng minh được: \(\widehat {ECO} + \widehat {OCD} + \widehat {BCD} = {180^0}\) Suy ra ba điểm E, C, B thẳng hàng. Lời giải chi tiết :
a) Xét tam giác AHO và tam giác BHO có: \(\widehat {AOH} = \widehat {BOH}\) (Ot là tia phân giác của \(\widehat {AOB}\)) OH chung \(\widehat {AHO} = \widehat {BHO}\left( { = {{90}^0}} \right)\) Suy ra \(\Delta AHO = \Delta BHO\left( {g.c.g} \right)\) Suy ra OA = OB (hai cạnh tương ứng) (đpcm) b) \(\Delta AHO = \Delta BHO\) suy ra AH = HB (hai cạnh tương ứng) Xét tam giác AHC và tam giác BHC có: HC chung \(\widehat {AHC} = \widehat {BHC}\left( { = {{90}^0}} \right)\) AH = HB Suy ra \(\Delta AHC = \Delta BHC\) (hai cạnh góc vuông) Suy ra \(\widehat {ACH} = \widehat {HCB}\) (hai góc tương ứng) c) Xét tam giác OCE và OCD có: OE = OD \(\widehat {EOC} = \widehat {DOC}\) OC chung Suy ra ∆OEC = ∆ODC (c.g.c) Suy ra EC = DC (hai cạnh tương ứng) Ta có OA = OB và OE = OD nên AE = BD. Xét \(\Delta ECA\) và \(\Delta DCB\) có: EC = ED (cmt) EA = DB (cmt) CA = CB (\(\Delta AHC = \Delta BHC\)) Suy ra \(\Delta ECA = \Delta DCB\) (c.c.c) Suy ra \(\widehat {ECA} = \widehat {DCB}\) (hai góc tương ứng) Mặt khác \(\widehat {ECA} + \widehat {ECD} = {180^0}\) (vì AC cắt Oy tại D) Suy ra \(\widehat {DCB} + \widehat {ECD} = {180^0}\) hay B, C, E thẳng hàng (đpcm). Phương pháp giải :
Đặt \(\frac{a}{b} = \frac{c}{d} = k\). Áp dụng dãy tỉ số bằng nhau để chứng minh. Lời giải chi tiết :
Đặt \(\frac{a}{b} = \frac{c}{d} = k \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = bk}\\{c = dk}\end{array}} \right.\) Do đó ta có: \(\frac{{ac}}{{bd}} = \frac{{bkdk}}{{bd}} = {k^2}(1)\) Ta cũng có: \(\frac{{{a^2} + {c^2}}}{{{b^2} + {d^2}}} = \frac{{{{(bk)}^2} + {{(dk)}^2}}}{{{b^2} + {d^2}}} = \frac{{{b^2}{k^2} + {d^2}{k^2}}}{{{b^2} + {d^2}}} = \frac{{{k^2}\left( {{b^2} + {d^2}} \right)}}{{{b^2} + {d^2}}} = {k^2}(2)\) Từ (1) và (2) suy ra: \(\frac{{ac}}{{bd}} = \frac{{{a^2} + {c^2}}}{{{b^2} + {d^2}}} = \left( {{k^2}} \right)\) (đpcm)
|

























Danh sách bình luận