Đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 7I. Trắc nghiệm Câu 1 : Một cửa hàng bán nước hoa quả đã khảo sát về các loại nước mà khách hàng ưa chuộng và thu được bảng dữ liệu sau:Đề bài
I. Trắc nghiệm
Câu 1 :
Một cửa hàng bán nước hoa quả đã khảo sát về các loại nước mà khách hàng ưa chuộng và thu được bảng dữ liệu sau:
Biểu đồ đoạn thẳng để biểu diễn cho các mặt hàng ưa chuộng là:
Câu 2 :
Khi được hỏi về môn học yêu thích của một nhóm bạn lớp cho kết quả được ghi lại trong bảng như sau:
Có bao nhiêu bạn được hỏi?
Câu 3 :
Bạn Nam gieo một con xúc xắc 10 lần liên tiếp thì thấy mặt 4 chấm xuất hiện 3 lần. Xác suất xuất hiện mặt 4 chấm là
Câu 4 :
An lấy ngẫu nhiên 4 viên bi trong một túi đựng 4 bi xanh và 3 bi đỏ. Đâu là biến cố chắc chắn?
Câu 5 :
Gieo một con xúc xắc đồng chất một lần. Xác suất xuất hiện mặt có số chấm chẵn là:
Câu 6 :
Cho tam giác ABC. Trong các khẳng định sau khẳng định nào sai?
Câu 7 :
Cho \(\Delta ABC = \Delta DEF\). Khi đó:
Câu 8 :
Cho \(\Delta ABC = \Delta DEF\), \(\hat C = {40^0}\). Khi đó:
Câu 9 :
Cho tam giác ABC có: \(\widehat A = {45^0};\widehat B = {60^0}\). So sánh các cạnh của tam giác ABC là:
Câu 11 :
Cho tam giác ABC cân tại A, cạnh AB = 5cm. Tính độ dài cạnh AC?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Một cửa hàng bán nước hoa quả đã khảo sát về các loại nước mà khách hàng ưa chuộng và thu được bảng dữ liệu sau:
Biểu đồ đoạn thẳng để biểu diễn cho các mặt hàng ưa chuộng là:
Đáp án : C Phương pháp giải :
Dựa vào đặc điểm của các loại biểu đồ. Lời giải chi tiết :
Biểu đồ đoạn thẳng là biểu đồ C.
Câu 2 :
Khi được hỏi về môn học yêu thích của một nhóm bạn lớp cho kết quả được ghi lại trong bảng như sau:
Có bao nhiêu bạn được hỏi?
Đáp án : B Phương pháp giải :
Dựa vào bảng thống kế để xác định. Lời giải chi tiết :
Trong bảng thống kê trên, ta thấy có 8 câu trả lời nên có 8 bạn được hỏi.
Câu 3 :
Bạn Nam gieo một con xúc xắc 10 lần liên tiếp thì thấy mặt 4 chấm xuất hiện 3 lần. Xác suất xuất hiện mặt 4 chấm là
Đáp án : B Phương pháp giải :
Xác suất bằng tỉ số giữa số lần xuất hiện mặt 4 chấm với tổng số lần gieo. Lời giải chi tiết :
Xác suất xuất hiện mặt 4 chấm là \(\frac{3}{{10}}\).
Câu 4 :
An lấy ngẫu nhiên 4 viên bi trong một túi đựng 4 bi xanh và 3 bi đỏ. Đâu là biến cố chắc chắn?
Đáp án : B Phương pháp giải :
Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra. Lời giải chi tiết :
Biến cố A. Biến cố ngẫu nhiên. Biến cố B. Biến cố chắc chắn. Biến cố C. Biến cố ngẫu nhiên. Biến cố D. Biến cố ngẫu nhiên.
Câu 5 :
Gieo một con xúc xắc đồng chất một lần. Xác suất xuất hiện mặt có số chấm chẵn là:
Đáp án : D Phương pháp giải :
Xác suất xuất hiện mặt có chấm chẵn bằng tỉ số giữa số số mặt có chấm chẵn với tổng số mặt của xúc xắc. Lời giải chi tiết :
Có 3 mặt có số chấm chẵn là 2; 4; 6. Số mặt của xúc xắc là 6: 1; 2; 3; 4; 5; 6. Xác suất xuất hiện mặt có số chấm chẵn là: \(\frac{3}{6} = \frac{1}{2}\).
Câu 6 :
Cho tam giác ABC. Trong các khẳng định sau khẳng định nào sai?
Đáp án : C Phương pháp giải :
Dựa vào quan hệ giữa ba cạnh của một tam giác. Lời giải chi tiết :
Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại nên A, B và D đúng. Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại nên C sai.
Câu 7 :
Cho \(\Delta ABC = \Delta DEF\). Khi đó:
Đáp án : A Phương pháp giải :
Dựa vào các kiến thức về hai tam giác bằng nhau. Lời giải chi tiết :
\(\Delta ABC = \Delta DEF\) nên ta có: \(\begin{array}{l}AB = DE\\BC = EF\\AC = DF\end{array}\)
Câu 8 :
Cho \(\Delta ABC = \Delta DEF\), \(\hat C = {40^0}\). Khi đó:
Đáp án : A Phương pháp giải :
Dựa vào các kiến thức về hai tam giác bằng nhau. Lời giải chi tiết :
\(\Delta ABC = \Delta DEF\) nên ta có: \(\widehat C = \widehat F = {40^0}\).
Câu 9 :
Cho tam giác ABC có: \(\widehat A = {45^0};\widehat B = {60^0}\). So sánh các cạnh của tam giác ABC là:
Đáp án : A Phương pháp giải :
Áp dụng định lí tổng ba góc của một tam giác và quan hệ giữa góc và cạnh đối diện trong một tam giác. Lời giải chi tiết :
Xét tam giác ABC có: \(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {45^0} - {60^0}\\ = {75^0}\end{array}\) Trong tam giác ABC, ta có: \(\widehat C > \widehat B > \widehat A\left( {{{75}^0} > {{60}^0} > {{45}^0}} \right)\) suy ra \(AB > AC > BC\).
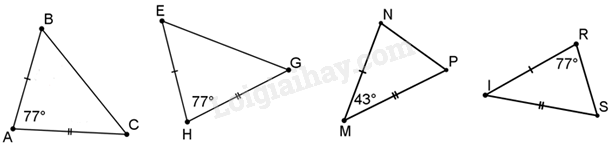
Đáp án : A Phương pháp giải :
Dựa vào các trường hợp bằng nhau của hai tam giác để xác định. Lời giải chi tiết :
Trong các tam giác trên, chỉ có \(\Delta ABC = \Delta HEG\)(c.g.c) đủ điều kiện để xác định bằng nhau.
Câu 11 :
Cho tam giác ABC cân tại A, cạnh AB = 5cm. Tính độ dài cạnh AC?
Đáp án : D Phương pháp giải :
Dựa vào tính chất của tam giác cân. Lời giải chi tiết :
Tam giác ABC cân tại A nên AB = AC = 5cm.
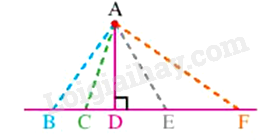
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về đường xiên. Lời giải chi tiết :
Trong hình trên, có 4 đường xiên là: AB, AC, AE, AF.
II. Tự luận
Phương pháp giải :
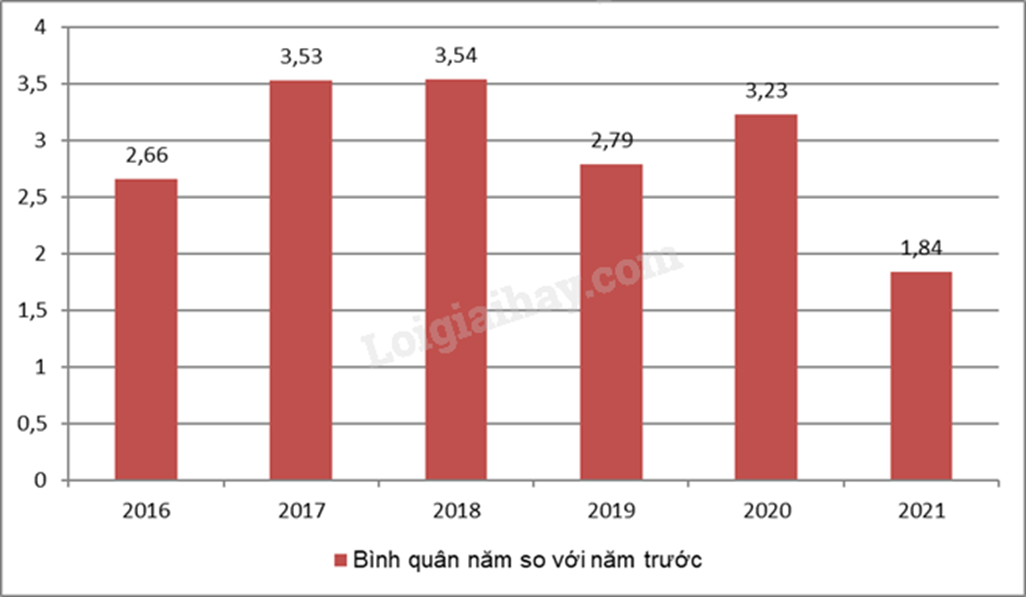
a, b) Quan sát biểu đồ để trả lời câu hỏi. c) CPI trung bình bằng tổng số CPI chia cho số năm. Lời giải chi tiết :
a) Bảng số liệu thống kê tốc độ tăng trưởng chỉ số tiêu dùng(CPI) các năm giai đoạn 2016-2021:
b) Năm có CPI trung bình lớn nhất là năm 2018 với CPI là 3,54%. c) CPI trung bình của các năm từ 2016 đến 2021 là: $\frac{2,66+3,53+3,54+2,79+3,23+1,84}{6}\approx 2,93$ Phương pháp giải :
Xác định số kết quả có thể, số kết quả thuận lợi cho biến cố. Lời giải chi tiết :
Có 12 kết quả có thể xảy ra khi rút ngẫu nhiên một thẻ trong hộp, đó là: 1; 2; 3; …; 12. Có 5 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ là số nguyên tố” là: 2; 3; 5; 7; 11. Vậy xác suất của biến cố ‘‘Số xuất hiện trên thẻ là số nguyên tố’’ là: \(\frac{5}{{12}}\). Phương pháp giải :
Dựa vào định lí tổng hai góc nhọn trong một tam giác vuông bằng \({90^0}\). Lời giải chi tiết :
Gọi tam giác ABC là hình mô tả chiếc thang dựa vào tường. Góc C là góc nghiêng của thang so với tường. Trong tam giác ABC vuông tại A có: \(\widehat B + \widehat C = {90^0}\) (tổng hai góc nhọn trong một tam giác vuông). Suy ra \(\widehat C = {90^0} - \widehat B = {90^0} - {50^0} = {40^0}\). Vậy độ nghiêng của chiếc thang so với bức tường là \({40^0}\). Phương pháp giải :
Áp dụng định lí tổng ba góc của một tam giác và quan hệ giữa góc và cạnh đối diện trong một tam giác. Lời giải chi tiết :
Xét tam giác ABC có: \(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {50^0} - {60^0}\\ = {70^0}\end{array}\) Trong tam giác ABC, ta có: \(\widehat C > \widehat B > \widehat A\left( {{{70}^0} > {{60}^0} > {{50}^0}} \right)\) suy ra \(AB > AC > BC\). Phương pháp giải :
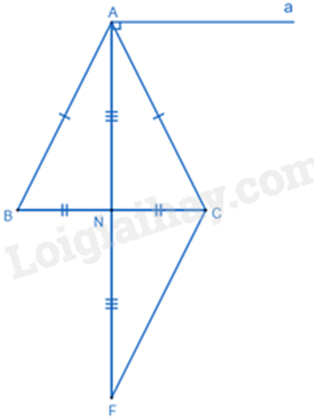
a) Dựa vào các trường hợp bằng nhau của hai tam giác. b) Chứng minh \(AN \bot BC\) suy ra a // BC. c) Dựa vào bất đẳng thức tam giác để chứng minh. Lời giải chi tiết :
a) Xét \(\Delta ABN\) và \(\Delta ACN\) có: \(\begin{array}{l}AB = AC(gt)\\BN = CN(gt)\\AN\,chung\end{array}\) Suy ra \(\Delta ABN = \Delta ACN\)(c.c.c) (đpcm) b) Ta có \(\Delta ABN = \Delta ACN\) suy ra \(\widehat {ANB} = \widehat {ANC}\). Mà hai góc này là hai góc kề bù nên \(\widehat {ANB} = \widehat {ANC} = \frac{{{{180}^0}}}{2} = {90^0}\). Do đó \(AN \bot BC\). Mà \(a \bot AN\) (gt) Suy ra \(a//BC\) (từ vuông góc đến song song) (đpcm). c) Xét \(\Delta ABN\) và \(\Delta FCN\) có: \(\begin{array}{l}AN = NF(gt)\\BN = CN(gt)\end{array}\) \(\widehat {ANB} = \widehat {FNC}\) (hai góc đối đỉnh) Suy ra \(\Delta ABN = \Delta FCN\)(c.g.c) (đpcm) Suy ra AB = CF. Xét \(\Delta ACF\) có: \(\begin{array}{l}CF + AC > AF\\AB + AC > 2AN\end{array}\) (vì AB = CF và AF = 2AN) (đpcm).
|





























Danh sách bình luận