Đề thi học kì 1 Toán 7 - Đề số 3 - Cánh diều

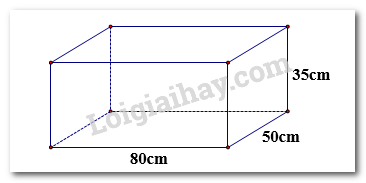
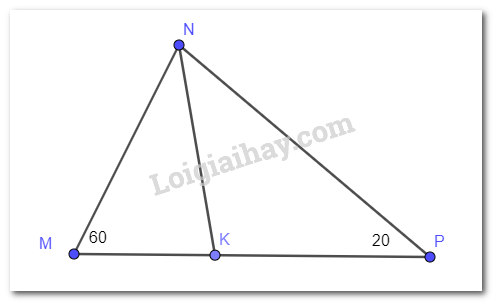
Đề bài

Phần I: Trắc nghiệm (3 điểm).

Câu 1: Nếu  \(\sqrt x  = 4\) thì  x bằng

     A. 2                                    B. 4                                    C. \( \pm \)2                 D. 16

Câu 2: Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 5 thì y = 15. Hệ số tỉ lệ  k của y đối với x là:

     A. 3                                    B. 75                                  C. \(\dfrac{1}{3}\)          D. 10

Câu 3: Trong các phân số sau đây, phân số nào biểu diễn số hữu tỉ \(\dfrac{{ - 1}}{2}\).

     A. \(\dfrac{{ - 2}}{4}\)          B. \(\dfrac{{ - 22}}{{48}}\)    C. \( - \dfrac{{ - 5}}{{10}}\)   D. \(\dfrac{{ - 6}}{{18}}\)

Câu 4: Cách viết nào dưới đây là đúng?

     A. \(\left| { - 0,55} \right| = 0,55\)                                  B. \(\left| {0,55} \right| =  - 0,55\)   C. \(\left| { - 0,55} \right| =  - 0,55\)             D. \( - \left| {0,55} \right| = 0,55\)

Câu 5: Cho \(x = 6,67254\). Khi làm tròn đến chữ số thập phân thứ ba thì số x là:

     A. \(6,672\)                        B. \(6,672\)                        C. \(6,67\)                     D. \(6,6735\)

Câu 6: Kết quả của phép tính:  \({\left( {\dfrac{1}{2}} \right)^2}.{\left( {\dfrac{1}{2}} \right)^3}\)bằng:

     A. \({\left( {\dfrac{1}{2}} \right)^2}.\)                            B. \({\left( {\dfrac{1}{2}} \right)^5}\)          C. \({\left( {\dfrac{1}{2}} \right)^3}\)                                        D. \(\dfrac{1}{2}\)

Câu 7: Cho hình lăng trụ dưới đây. Chọn đáp án sai:

     A. Hình lăng trụ đứng có tất cả 6 mặt                        

     B. Hình lăng trụ đứng có tất cả 8 đỉnh

     C. Hình lăng trụ đứng có tất cả 12 cạnh                     

     D. Hình lăng trụ đứng có 6 mặt bên

Câu 8: Cho a\( \bot \)b và b\( \bot \)c thì:

     A. a // b                              B. a // c                              C. b // c                         D. a // b // c

Câu 9:  Tam giác MNP có \(\angle M = {60^0}\), \(\angle N = {20^0}\), NK là tia phân giác. Số đo của góc \(\widehat {NKP}\) bằng:

     A. 110                                B. 100                                C. 70                             D. 30

Câu 10: Cho hình hộp chữ nhật có kích thước như hình vẽ. Diện tích toàn phần hình hộp chữ nhật là:

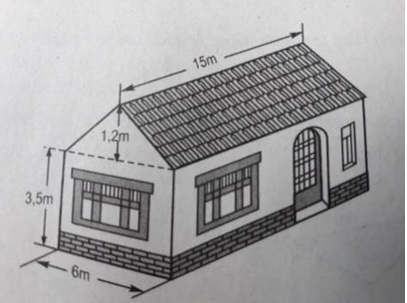
     A. 140000                          B. 4000                              C. 260                           D. 9100

Phần II: Tự luận (7 điểm).

Câu 1: (2 điểm) Thực hiện phép tính:

a. \(\dfrac{2}{7} + \left( {\dfrac{{ - 17}}{7}} \right) + \dfrac{8}{7}\)                                               b. \(\dfrac{5}{9}:\left( {\dfrac{1}{{11}} - \dfrac{5}{{22}}} \right) + \dfrac{5}{9}:\left( {\dfrac{1}{{15}} - \dfrac{2}{3}} \right).\)                   

c. \(\dfrac{{{{\left( { - 2} \right)}^3}}}{5}.\left| {\dfrac{1}{4} - 1} \right| + {2023^0}\).                    d. \( - \dfrac{5}{2}.\sqrt {\dfrac{9}{{25}}}  - {2^2}.\left| { - \dfrac{1}{4}} \right|\)

Câu 2: (1,5 điểm) Tìm x

     a. \(\,x + 1\dfrac{1}{2} =  - 5,6\)                                                b. \(\,\,\left| {x - \dfrac{1}{4}} \right| = \dfrac{5}{4}\)                                    c. \({\left( {\dfrac{1}{5} - \dfrac{3}{2}x} \right)^2} = \dfrac{9}{4}\)

Câu 3: (1,5 điểm) Ba lớp 7A, 7B và 7C đi lao động và được phân công khối lượng công việc như nhau. Lớp 7A hoàn thành công việc trong 3 giờ, lớp 7B hoàn thành công việc trong 4 giờ và lớp 7C hoàn thành công việc trong 5 giờ. Tính số học sinh của mỗi lớp, biết rằng tổng số học sinh của ba lớp là 94 học sinh (giả sử năng suất làm việc của mỗi học sinh đều như nhau).

Câu 4: (1,5 điểm) Tính thể tích phần không gian của ngôi nhà có dạng một lăng trụ đứng theo các kích thước đã  cho ở hình vẽ sau.

Câu 5: (0,5 điểm) So sánh \({2^{30}} + {3^{30}} + {4^{30}}\) và \({3.24^{10}}\)

Lời giải

I. Phần trắc nghiệm (3 điểm)

Câu 1

Phương pháp:

Chỉ tồn tại căn bậc hai số học của số x không âm.

Cách giải:

\(\sqrt x  = 4 \Leftrightarrow x = 16\)

Chọn D.

Câu 2

Phương pháp:

Nếu y liên hệ với x theo công thức y = k.x thì y tỉ lệ thuận với x theo k.

Cách giải:

Ta có y = 3. x nên k = 3

Chọn A.

Câu 3

Phương pháp:

Số đối của a là - a

Cách giải:

Số đối của \(\dfrac{{ - 1}}{2}\) là \(\dfrac{1}{2} =  - \dfrac{{ - 5}}{{10}}\)

Chọn C.

Câu 4

Phương pháp:

\(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,khi\,\,x \ge 0\\ - x\,\,khi\,\,x < 0\end{array} \right.\)

Cách giải:

\(\left| { - 0,55} \right| = 0,55\)

Chọn A.

Câu 5

Phương pháp:

So sánh số thập phân thứ 4 với số 5.

Cách giải:

Số thập phân thứ 3 là 2 và số thập phân thứ 4 là số 5 nên kết quả làm tròn bằng 6,672

Chọn B.

Câu 6

Phương pháp:

\({a^m}.{a^n} = {a^{m + n}}\)

Cách giải:

\({\left( {\dfrac{1}{2}} \right)^2}.{\left( {\dfrac{1}{2}} \right)^3} = {\left( {\dfrac{1}{2}} \right)^{2 + 3}} = {\left( {\dfrac{1}{2}} \right)^5}\)

Chọn B.

Câu 7

Phương pháp:

Hình lăng trụ đứng có 6 mặt, 8 đỉnh, 12 cạnh, 4 mặt bên, 2 mặt đáy

Cách giải:

Hình lăng trụ đứng có 6 mặt, 8 đỉnh, 12 cạnh, 4 mặt bên, 2 mặt đáy.

Chọn D.

Câu 8

Phương pháp:

Định lý từ vuông góc đến song song

Cách giải:

Vì a và c cùng vuông góc với b nên ta suy ra a // c.

Chọn B.

Câu 9

Phương pháp:

Dùng tính chất của tia phân giác

Cách giải:

 \(\begin{array}{l}\angle MNP = {180^0} - \angle N - \angle P = 180 - 60 - 20 = 100\\ \Rightarrow \angle MNK = 100:2 = 50\\ \Rightarrow \angle MKN = \angle M + \angle MNK = 60 + 50 = 110\end{array}\)

Chọn A.

Câu 10

Phương pháp:

Diện tích toàn phần hình hộp chữ nhật bằng chu vi đáy nhân chiều cao.

Cách giải:

Diện tích toàn phần bằng (80 + 50).2.35 = 9100

Chọn D.

II. Phần tự luận (7 điểm)

Câu 1

Phương pháp:

Áp dụng tính toán theo thứ tự thực hiện phép tính.

Cách giải:

a. \(\dfrac{2}{7} + \left( {\dfrac{{ - 17}}{7}} \right) + \dfrac{8}{7}\)\( = \dfrac{{2 + ( - 17) + 8}}{7} = \dfrac{{ - 7}}{7} =  - 1\)

b. \(\dfrac{5}{9}:\left( {\dfrac{1}{{11}} - \dfrac{5}{{22}}} \right) + \dfrac{5}{9}:\left( {\dfrac{1}{{15}} - \dfrac{2}{3}} \right) = \dfrac{5}{9}:\dfrac{{ - 3}}{{22}} + \dfrac{5}{9}:\dfrac{{ - 3}}{5} = \dfrac{5}{9}.\dfrac{{ - 22}}{3} + \dfrac{5}{9}.\dfrac{{ - 5}}{3}\)

\( = \left( {\dfrac{{ - 22}}{3} + \dfrac{{ - 5}}{3}} \right).\dfrac{5}{9} = ( - 9).\dfrac{5}{9} =  - 5\)

c. \(\dfrac{{{{\left( { - 2} \right)}^3}}}{5}.\left| {\dfrac{1}{4} - 1} \right| + {2023^0} = \dfrac{{ - 8}}{5}.\left| {\dfrac{{ - 3}}{4}} \right| + 1\)\( = \dfrac{{ - 8}}{5}.\dfrac{3}{4} + 1 = \dfrac{{ - 6}}{5} + 1 = \dfrac{{ - 1}}{5}\)

d. \( - \dfrac{5}{2}.\sqrt {\dfrac{9}{{25}}}  - {2^2}.\left| { - \dfrac{1}{4}} \right|\)=\( - \dfrac{5}{2}.\dfrac{3}{5} - 4.\dfrac{1}{4}\)=\( - \dfrac{3}{2} - 1\)=\( - \dfrac{5}{2}\)

Câu 2

Phương pháp:

\(\left| x \right| = a\,\) với \((a > 0)\)\( \Leftrightarrow \left[ \begin{array}{l}x = a\\x =  - a\end{array} \right.\)

\({x^2} = a\,\)với \((a > 0)\) \( \Leftrightarrow \left[ \begin{array}{l}x = \sqrt a \\x =  - \sqrt a \end{array} \right.\)

Cách giải:

a. \(x + 1\dfrac{1}{2} =  - 5,6 \Leftrightarrow x + 1,5 =  - 5,6 \Leftrightarrow x =  - 5,6 - 1,5 \Leftrightarrow x = \, - 7,1\)

b. \(\,\,\left| {x - \dfrac{1}{4}} \right| = \dfrac{5}{4} \Rightarrow \left[ \begin{array}{l}x - \dfrac{1}{4} = \dfrac{5}{4}\\x - \dfrac{1}{4} =  - \dfrac{5}{4}\end{array} \right. \Rightarrow \left[ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{2}\\x\,\,\,\,\,\,\,\,\,\,\, =  - 1\end{array} \right.\)

c. \({\left( {\dfrac{1}{5} - \dfrac{3}{2}x} \right)^2} = \dfrac{9}{4} \Rightarrow \left[ \begin{array}{l}\dfrac{1}{5} - \dfrac{3}{2}x = \dfrac{3}{2}\\\dfrac{1}{5} - \dfrac{3}{2}x = \dfrac{{ - 3}}{2}\end{array} \right. \Rightarrow \left[ \begin{array}{l}\dfrac{3}{2}x = \dfrac{1}{5} - \dfrac{3}{2}\\\dfrac{3}{2}x = \dfrac{1}{5} - \dfrac{{ - 3}}{2}\end{array} \right. \Rightarrow \left[ \begin{array}{l}\dfrac{3}{2}x = \dfrac{{ - 13}}{{10}}\\\dfrac{3}{2}x = \dfrac{{17}}{{10}}\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \dfrac{{ - 13}}{{15}}\\x = \dfrac{{17}}{{15}}\end{array} \right.\)

Câu 3

Phương pháp:

Đưa về dãy tỉ số bằng nhau.

Cách giải:

Gọi a, b, c lần lượt là số HS của 3 lớp 7A, 7B, 7C  (a,b,c \( \in \) N^* ; a, b, c < 94)

Do khối lượng công việc của ba lớp là như nhau nên số HS và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch. Khi đó ta có: 3a = 4b = 5c và a + b + c = 94

\(3a  =  4b  =  5c\,\, \Leftrightarrow \,\,\dfrac{a}{{20}} = \dfrac{b}{{15}} = \dfrac{c}{{12}}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\dfrac{a}{{20}} = \dfrac{b}{{15}} = \dfrac{c}{{12}} = \dfrac{{a + b + c}}{{20 + 15 + 12}} = \dfrac{{94}}{{47}} = 2\)

\(\begin{array}{l} \Rightarrow a = 2.20 = 40\\ \Rightarrow b = 2.15 = 30\\ \Rightarrow c = 2.12 = 24\end{array}\)

Vậy số của ba lớp 7A, 7B, 7C lần lượt là : 40, 30, 24.

Câu 4

Phương pháp:

Cần chia ngôi nhà ra làm hai phần:

+ Một phần là lăng trụ đứng: Đáy của lăng trụ này là tam giác cân, cạnh đáy 6m , chiều cao của đáy 1,2m, chiều cao lăng trụ 15m .

+ Phần còn lại là hình hộp chữ nhật: Có chiều dài 15m , rộng 6m , cao 3,5m .

Cách giải:

Cần chia ngôi nhà ra làm hai phần:

+ Một phần là lăng trụ đứng: Đáy của lăng trụ này là tam giác cân, cạnh đáy 6, chiều cao của  đáy 1,2m; chiều cao lăng trụ 15m.

+ Phần còn lại là hình hộp chữ nhật: Có chiều dài 15m , rộng 6m , cao 3,5m

Diện tích đáy của lăng trụ có đáy là tam giác là:  1,2.6:2=3,6\({m^2}\)

Thể tích lăng trụ có đáy tam giác là: 15.3,6=54\({m^2}\)

Thể tích đáy hình chữ nhật là: 3,5.6=21\({m^2}\)

Thể tích hình hộp chữ nhật là 21. 15=315\({m^2}\)

Vậy thể tích ngôi nhà là 315 + 54 = 369\({m^2}\)

Câu 5

Phương pháp:

Đưa về lũy thừa cùng cơ số hoặc cùng số mũ để so sánh.

Cách giải:

Ta có: \({4^{30}} = {2^{30}}{.2^{30}} = {\left( {{2^3}} \right)^{30}}.{\left( {{2^2}} \right)^{15}} > {8^{10}}{.3^{15}} > \left( {{8^{10}}{{.3}^{10}}} \right).3 > {24^{10}}.3\)                  

Vậy \({2^{30}} + {3^{30}} + {4^{30}}\) > \({3.24^{10}}\).