Bài tập 5 trang 96 Tài liệu dạy – học Toán 7 tập 2Giải bài tập Cho tam giác ABC nhọn (AB < AC) Quảng cáo
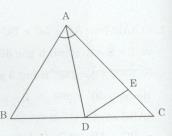
Đề bài Cho tam giác ABC nhọn (AB < AC). Tia phân giác của \(\widehat {BAC}\) cắt BC ở D. Trên tia AC lấy điểm E sao cho AE = AB. a) Chứng minh: \(\widehat {DEC} > \widehat {ADB}\) b) So sánh độ dài BD và DC. Lời giải chi tiết
a) Xét ∆ADE và ∆ADB ta có: AE = AB (gt) \(\widehat {DAE} = \widehat {BAD}\) (AD là tia phân giác của \(\widehat {BAC}\)) AD (cạnh chung) Do đó ∆ADE = ∆ADB (c.g.c) \( \Rightarrow \widehat {ADE} = \widehat {ADB}\) Mà \(\widehat {DEC}\) là góc ngoài của tam giác ADE Nên \(\widehat {DEC} > \widehat {ADE} \Rightarrow \widehat {DEC} > \widehat {ADB}.\) b) Ta có \(\widehat {ADB} > \widehat {DCE}(\widehat {ADB}\) là góc ngoài của tam giác ACD) Mà \(\widehat {DEC} > \widehat {ADB}\) (câu a) \( \Rightarrow \widehat {DEC} > \widehat {DCE}\) ∆CDE có \(\widehat {DEC} > \widehat {DCE} \Rightarrow\) DC > ED (định lí cạnh đối diện với góc lớn hơn) Mà ED = BD (∆ADE = ∆ADB). Do vậy DC>BD. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
|
