Bài tập 34 trang 98 Tài liệu dạy – học Toán 7 tập 2Giải bài tập Cho tam giác ABC vuông tại A có M là trung điểm của AC. Gọi E và F lần lượt là hình chiếu kẻ từ A và C đến các đường thẳng BM. Quảng cáo
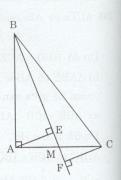
Đề bài Cho tam giác ABC vuông tại A có M là trung điểm của AC. Gọi E và F lần lượt là hình chiếu kẻ từ A và C đến các đường thẳng BM. Chứng minh: \(AB < {{BE + BF} \over 2} < BC\) Lời giải chi tiết
Xét ∆AEM vuông tại E và ∆MCF vuông tại F ta có: AM = MC (M là trung điểm của AC) Và \(\widehat {EMA} = \widehat {CMF}\) (hai góc đối đỉnh) Do đó: ∆AEM = ∆CFM (cạnh huyền – góc nhọn) => EM = MF BE + BF = BE + BM + MF = BE + BM + EM (vì MF = EM) = (BE + EM) + BM = BM + BM = 2BM Do đó \(BM = {{BE + BF} \over 2}(1)\) Mà \(BA \bot AC\) tại A, Mặt khác, ta có AM < AC => BM < BC (3) Từ (1), (2) và (3) ta có: \(AB < {{BE + BF} \over 2} < BC.\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
