Bài 8 trang 169 Tài liệu dạy – học Toán 7 tập 1Giải bài tập Cho tam giác DEF cân tại D. Gọi H là trung điểm của EF. Quảng cáo
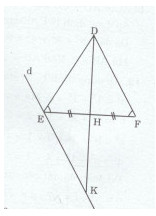
Đề bài Cho tam giác DEF cân tại D. Gọi H là trung điểm của EF. a) Chứng minh rằng DH là phân giác của \(\widehat {EDF}.\) b) Từ E kẻ đường thẳng d song song với DF, d cắt đường thẳng DH tại K. Chứng minh rằng tam giác DEK cân. Lời giải chi tiết a)Xét tam giác DEH và DFH ta có: DH là cạnh chung. DE = DF (tam giác DEF cân tại D) HE = HF (H là trung điểm của EF) Do đó: \(\eqalign{ & \Delta DEH = \Delta DFH(c.c.c) \cr & \Rightarrow \widehat {EDH} = \widehat {FDH} \cr} \) Vậy DH là tia phân giác của góc EDF. b) Ta có: \(\widehat {EKD} = \widehat {FDH}\) (so le trong và EK // DF) Mà \(\widehat {EDK} = \widehat {FDH}(cmt)\) Do đó: \(\widehat {EKD} = \widehat {EDK}\) Vậy tam giác DEK cân tại E.\)AB = \sqrt {11} \) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
