Bài 7 trang 33 SGK Toán 11 tập 1 - Chân trời sáng tạo

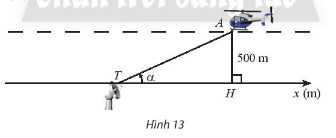
Đề bài

Trong Hình 13, một chiếc máy bay A bay ở độ cao 500m theo một đường thẳng đi ngang qua phía trên trạm quan sát T ở mặt đất. Hình chiếu vuông góc của A lên mặt đất là H, \(\alpha \) là góc lượng giác \((Tx,{\rm{ }}TA)\) \((0 < \alpha  < \pi ).\)

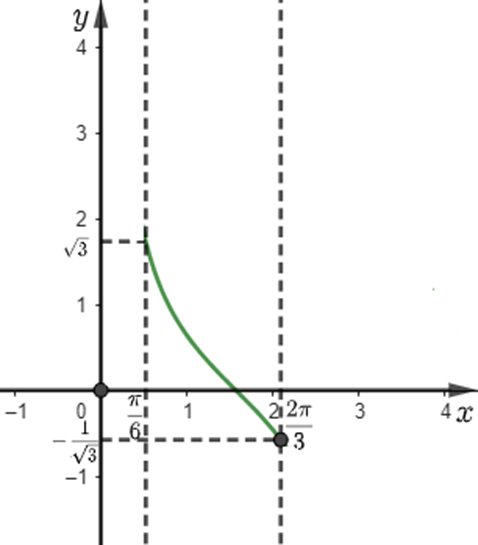
a) Biểu diễn toạ độ \({x_H}\) của điểm H trên trục \({T_x}\) theo \(\alpha \).

b) Dựa vào đồ thị hàm số côtang, hãy cho biết với \(\frac{\pi }{6} < \alpha  < \frac{{2\pi }}{3}\) thì \({x_H}\) nằm trong khoảng nào. Làm tròn kết quả đến hàng phần mười.

Lời giải chi tiết

a) Xét tam giác AHT vuông tại H có:

\(\cot \alpha  = \frac{{TH}}{{AH}} \Leftrightarrow TH = AH.\cot \alpha  = 500.\cot \alpha \).

Vậy trên trục \({T_x}\) tọa độ \({x_H} = 500.\cot \alpha \).

b) Ta có \(\cot \frac{\pi }{6} = \sqrt 3 \); \(\cot \frac{{2\pi }}{3} =  - \frac{1}{{\sqrt 3 }}\).

Đồ thị của hàm số \(y = \cot\alpha \) trong khoảng \(\frac{\pi }{6} < \alpha  < \frac{{2\pi }}{3}\) là:

Khi đó \(-\frac{1}{{\sqrt 3 }} < \cot\alpha  < \sqrt 3  \Leftrightarrow -\frac{{500}}{{\sqrt 3 }} < 500.\cot\alpha  < 500\sqrt 3\)

\( \Leftrightarrow -\frac{{500}}{{\sqrt 3 }} < {x_H} < 500\sqrt 3 \Leftrightarrow  - 288,7 < {x_H} < 866\).

Vậy \({x_H} \in \{  - 288,7;866\} \).