Bài 6 trang 33 SGK Toán 11 tập 1 - Chân trời sáng tạo

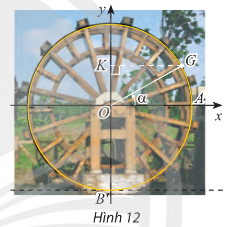
Đề bài

Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng 3m. Xét gàu G của guồng. Ban đầu gàu G nằm ở vị trí A (Hình 12)

a) Viết hàm số h biểu diễn chiều cao (tính bằng mét) của gàu G so với mặt nước theo góc $\alpha  = (OA,OG)$

b) Guồng nước quay hết mỗi vòng trong 30 giây. Dựa vào đồ thị của hàm số sin, hãy cho biết ở các thời điểm t nào trong 1 phút đầu, khoảng cách của gàu đến mặt nước bằng 1,5m.

Lời giải chi tiết

a) Điểm G là điểm biểu diễn cho góc lượng giác có số đo $\alpha$. Khi đó tọa độ điểm $G\left( {3cos\alpha ;{\rm{ }}3sin\alpha } \right)$.

Chiều cao của gàu ở vị trí G đến mặt nước là: $3{\rm{ }} + {\rm{ }}3sin\alpha$ (m).

b) b) Khoảng cách của gàu đến mặt nước bằng 1,5m khi $3 + 3sin\alpha  = 1,5 \Leftrightarrow sin\alpha {\rm{ }} = \frac{{ - 1}}{2}$

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\alpha  = \frac{{ - \pi }}{6} + k2\pi }\\{\alpha  = \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.$

Một vòng quay là 30 giây và t nằm trong khoảng từ 0 đến 1 phút do đó t ∈ [0; 2π].

Guồng quay mỗi vòng trong 30 giây nên 1 phút guồng quay được 2 vòng, tương ứng với $4\pi$. Vậy khi gàu cách mặt nước 1,5m thì $\alpha  = \frac{{7\pi }}{6},\alpha  = \frac{{19\pi }}{6},\alpha  = \frac{{11\pi }}{6},\alpha  = \frac{{23\pi }}{6}.$

Guồng quay 1 vòng tương đương với góc $2\pi$ hết 30 giây nên để quay hết $\frac{\pi }{6}$ vòng mất 2,5 giây.

Guồng quay 1 góc $\alpha  = \frac{{7\pi }}{6}$ hết 17,5 giây.

Guồng quay 1 góc $\alpha  = \frac{{19\pi }}{6}$ hết 47,5 giây.

Guồng quay 1 góc $\alpha  = \frac{{11\pi }}{6}$ hết 27,5 giây.

Guồng quay 1 góc $\alpha  = \frac{{23\pi }}{6}$ hết 57,5 giây.

Vậy, ở thời điểm t bằng 17,5 giây, 27,5 giây, 47,5 giây và 57,5 giây, gàu ở cách mặt nước 1,5m.