Bài 38 trang 10 SBT Hình học 12 Nâng caoGiải bài 38 trang 10 sách bài tập Hình học 12 Nâng cao. Cho tứ diện ABCD. Gọi d là khoảng cách giữa hai đường thẳng AB và CD... Quảng cáo
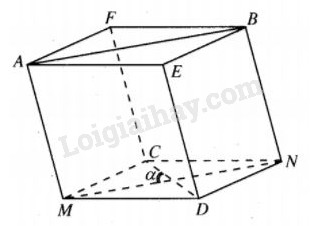
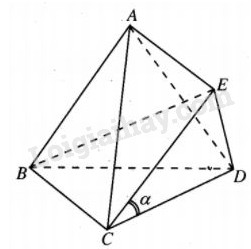
Đề bài Cho tứ diện ABCD. Gọi d là khoảng cách giữa hai đường thẳng AB và CD, \(\alpha \) là góc giữa hai đường thẳng đó. Chứng minh rằng \({V_{ABCD}} = {1 \over 6}AB.CD.d.\sin \alpha .\) Lời giải chi tiết Cách 1:
Dựng hình hộp AEBF.MDNC ( gọi là hình hộp ngoại tiếp tứ diện ABCD). Vì \(\left( {AEBF} \right)//\left( {MDNC} \right)\) nên chiều cao của hình hộp bằng khoảng cách d giữa AB và CD. Theo bài 37 ta có : \({V_{ABCD}} = {1 \over 3}\) Vhộp \(\eqalign{ & = {1 \over 3}{S_{MDNC}}.d \cr & = {1 \over 3}.{1 \over 2}MN.CD\sin \alpha .d = {1 \over 6}AB.CD.d\sin \alpha . \cr} \) Cách 2.
Dựng hình bình hành ABCE . Khi đó : \({V_{A.BCD}} = {V_{E.BCD}}\) (do \(AE//\left( {BCD} \right)\)) (1) \(\eqalign{ & {V_{E.BCD}} = {V_{B.ECD}}\;\;\;\;\;(2) \cr & {V_{B.ECD}} = {1 \over 3}{S_{ECD}}.d\left( {B,\left( {CDE} \right)} \right)\;\;\;(3) \cr & \cr} \) \({S_{ECD}} = {1 \over 2}CE.CD.\sin \widehat {ECD}\) \(= {1 \over 2}AB.CD\sin \alpha \;\;\;\;\;\;\;\;\;\;\;\;(4) \) \(d\left( {B,\left( {CDE} \right)} \right) = d\left( {AB,CD} \right)(\) do \(AB//\left( {CDE} \right))\;(5)\) Từ (1), (2), (3), (4), (5) suy ra : \({V_{ABCD}} = {1 \over 6}AB.CD.d\sin \alpha .\) Loigiaihay.com
|




















Danh sách bình luận