Bài 43 trang 11 SBT Hình học 12 Nâng caoGiải bài 43 trang 11 sách bài tập Hình học 12 Nâng cao. Khối chóp S.ABCD có đáy là hình bình hành... Quảng cáo
Đề bài Khối chóp S.ABCD có đáy là hình bình hành. Gọi B’, D’ lần lượt là trung điểm của SB, SD. Mặt phẳng \(\left( {AB'D'} \right)\) cắt SC tại C’. Tìm tỉ số thể tích của hai khối chóp S.AB’C’D’ và S.ABCD. Lời giải chi tiết
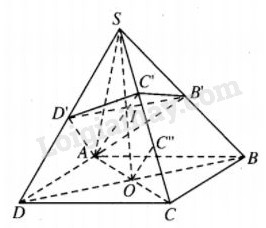
Dễ thấy \(AC',B'D'\) và \(SO\left( {O = AC \cap BD} \right)\) đồng quy tại \(I\) và \(I\) là trung điểm của SO. Kẻ \(OC''//AC'.\) Dễ thấy \(SC' = C'C'' = C''C.\) Vậy \({{SC'} \over {SC}} = {1 \over 3}.\) Ta có \(\eqalign{ & {{{V_{S.AB'C'}}} \over {{V_{S.ABC}}}} = {{SB'} \over {SB}}.{{SC'} \over {SC}} = {1 \over 2}.{1 \over 3} = {1 \over 6} \cr & \Rightarrow {{{V_{S.AB'C'}}} \over {{V_{S.ABCD}}}} = {1 \over {12}}. \cr} \) Chứng minh tương tự, ta cũng có : \({{{V_{S.AC'D'}}} \over {{V_{S.ABCD}}}} = {1 \over {12}}.\) Vậy \({{{V_{S.AB'C'D'}}} \over {{V_{S.ABCD}}}} = {{{V_{S.AB'C'}} + {V_{S.AC'D'}}} \over {{V_{S.ABCD}}}} = {1 \over 6}.\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
|
