Bài 41 trang 10 SBT Hình học 12 Nâng cao

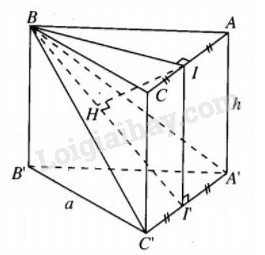
Đề bài

Cho khối lăng trụ tam giác \(ABC.A'B'C'\) có cạnh đáy bằng a, chiều cao bằng h. Tính thể tích khối chóp A.BC’A’.

Lời giải chi tiết

Cách 1:

\(AC//A'C' \Rightarrow AC//\left( {BC'A'} \right).\) Gọi I là trung điểm của AC thì

\(d\left( {A,\left( {BC'A'} \right)} \right) = d\left( {I,\left( {BC'A'} \right)} \right).\)

Gọi I’ là trung điểm của A’C’ thì rõ ràng \(BI' \bot A'C',\) mặt khác \(II' \bot A'C'\) nên \(A'C' \bot \left( {IBI'} \right).\)

Vậy khi ta hạ \(IH \bot BI'\) thì \(A'C' \bot IH.\)

Từ đó suy ra \(IH \bot \left( {BC'A'} \right),\) tức là \(d\left( {A,\left( {BC'A'} \right)} \right) = IH.\)

Ta có :

\(\eqalign{  & IH = {{IB.II'} \over {BI'}} = {{a.{{\sqrt 3 } \over 2}.h} \over {\sqrt {3.{{{a^2}} \over 4} + {h^2}} }} = {{\sqrt 3 ah} \over {\sqrt {3{a^2} + 4{h^2}} }},  \cr  & {S_{BC'A'}} = {1 \over 2}BI'.C'A' = {1 \over 2}\sqrt {{{3{a^2}} \over 4} + {h^2}} .a \cr&\;\;\;\;\;\;\;\;\;\;\;= {1 \over 4}a\sqrt {3{a^2} + 4{h^2}} . \cr} \)

Vậy

\({V_{A.BC'A'}} = {1 \over 3}.{1 \over 4}.a.\sqrt {3{a^2} + 4{h^2}} .{{\sqrt 3 ah} \over {\sqrt {3{a^2} + 4{h^2}} }} = {{\sqrt 3 {a^2}h} \over {12}}\)

Cách 2.

\(\eqalign{ &   {V_{A.BC'A'}} = {V_{B.AA'C'}} = {1 \over 2}.{V_{B.AA'C'C}} \cr&= {1 \over 2}.{2 \over 3}.{V_{ABC.A'B'C'}}  \cr  &  = {1 \over 3}.{S_{ABC}}.h\cr& = {1 \over 3}.{{{a^2}\sqrt 3 } \over 4}.h = {{{a^2}\sqrt 3 } \over {12}}.h \cr} \)

Loigiaihay.com