Bài 42 trang 11 SBT Hình học 12 Nâng cao

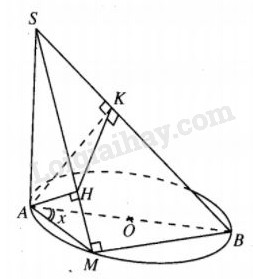
Đề bài

Cho đường tròn đường kính AB nằm trên mặt phẳng \(\left( P \right)\) và một điểm M di động trên đường tròn. Trên đường thẳng vuông góc với \(mp\left( P \right)\) tại A, lấy một điểm S. Mặt phẳng \(\left( Q \right)\) qua A vuông góc với SB tại K cắt SM tại H. Tìm vị trí của M để tính thể tích khối chóp S.AHK lớn nhất. Chứng minh rằng khi đó cung AM nhỏ hơn cung BM.

Lời giải chi tiết

\(\eqalign{  & MB \bot AM,MB \bot SA  \cr  &  \Rightarrow MB \bot \left( {SAM} \right) \Rightarrow MB \bot AH(1)  \cr  & SB \bot \left( {AKH} \right) \Rightarrow SB \bot AH.(1) \cr} \)

Từ (1) và (2) suy ra \(\eqalign{  & AH \bot \left( {SMB} \right) \Rightarrow AH \bot SM,AH \bot HK.  \cr  & {V_{S.AHK}} = {1 \over 3}{S_{AHK}}.SK = {1 \over 6}AH.KH.SK. \cr} \)

Vì \(SK\) cố định nên :

\({V_{S.AHK}}\max  \Leftrightarrow \left( {AH.KH} \right)\max  \)

\(\Leftrightarrow \left( {A{H^2}.K{H^2}} \right)\max  \Leftrightarrow A{H^2} = K{H^2} = {{A{K^2}} \over 2}\)

( vì \(A{H^2} + H{K^2} = A{K^2}\) không đổi).

Vậy ta chỉ cần xác định vị trí điểm M thỏa mãn điều kiện \(A{H^2} = {{A{K^2}} \over 2}.\left(  *  \right)\)

Đặt \(\widehat {MAB}\) =x,SA=h, AB=2R. Ta có

\(\eqalign{  & A{K^2} = {{S{A^2}.A{B^2}} \over {S{B^2}}} = {{4{R^2}{h^2}} \over {4{R^2} + {h^2}}},  \cr  & AM = 2R{\mathop{\rm cosx}\nolimits} ,  \cr  & A{H^2} = {{S{A^2}.A{M^2}} \over {S{M^2}}} = {{4{h^2}{R^2}{{\cos }^2}x} \over {{h^2} + 4{R^2}{{\cos }^2}x}}. \cr} \)

Từ \(\left(  *  \right)\) ta suy ra : \({\cos ^2}x = {{{h^2}} \over {2\left( {{h^2} + 2{R^2}} \right)}} < {1 \over 2}.\)

Từ đây ta xác định được x, tức là xác định được vị trí điểm M (có hai vị trí của điểm M ).

Từ \({\cos ^2}x < {1 \over 2}\) suy ra \({\mathop{\rm cosx}\nolimits}  < {{\sqrt 2 } \over 2} = \cos {45^0} \Rightarrow x > {45^0}  \).

Vậy cung BM lớn hơn cung AM

Loigiaihay.com