Bài 32 trang 10 SBT Hình học 12 Nâng cao

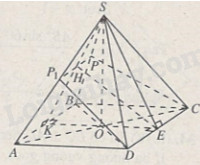
Đề bài

Cho khối chóp tứ giác đều \(S.ABCD\) mà trung đoạn của nó ( đường cao của một mặt bên hạ từ đỉnh hình chóp) bằng 6 còn góc giữa hai mặt bên dối diện bằng \({60^0}\). Qua CD, dựng mặt phẳng \(\left( \alpha  \right)\) vuông góc với \(mp\left( {SAB} \right)\), cắt SA, SB lần lượt tại P₁ và P.

Hãy tính thể tích khối chóp S.CDP₁P.

Lời giải chi tiết

Giả sử SK và SE là hai trung đoạn của khối chóp.

Vì \(CD//AB\) nên giao tuyến \(\Delta \) của hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {SAB} \right)\) song song với CD và AB.

Ta có \(SE \bot CD;SK \bot AB \Rightarrow SE \bot \Delta ,SK \bot \Delta  \Rightarrow \) \(\widehat {KSE}\) là góc giữa hai mặt phẳng (SCD) và (SAB).

Vậy \(\widehat {KSE}\) = 60⁰.

Do \(CD//AB\) nên giao tuyến P₁P của \(\left(\alpha \right)\) và \(\left( {SAB} \right)\)song song với \(CD\) và \(AB\).

Tứ đó dễ thấy tứ giác CDP₁P là hình thang cân và EH là đường cao của nó \(\left( {H = SK \cap {P_1}P} \right)\).

Ta có \(EH \bot {P_1}P,\) mà \({P_1}P = \left( \alpha  \right) \cap \left( {SAB} \right),\left( \alpha  \right) \bot \left( {SAB} \right)\) nên suy ra \(EH \bot \left( {SAB} \right) \Rightarrow EH \bot SH.\)

Mặt khác \(SH \bot {P_1}P \Rightarrow SH \bot \left( {CD{P_1}P} \right)\) nên SH là đường cao của hình chóp S.CDP₁P.

Tam giác SKE cân đỉnh S và có góc ở đỉnh bằng 60⁰ nên nó là tam giác đều.

Vậy H là trung điểm của SK, suy ra

\({P_1}P = {1 \over 2}AB = {1 \over 2}KE = {1 \over 2}SE = {1 \over 2}.6 = 3.\)

Ta có :

\(\eqalign{&
{V_{S.CD{P_1}P}} = {1 \over 3}{S_{CD{P_1}P}}.SH \cr&= {1 \over 3} \cdot {1 \over 2}\left( {CD + {P_1}P} \right).EH.SH \cr 
& ={1 \over 6}\left( {6 + 3} \right) \cdot {{6\sqrt 3 } \over 2} \cdot 3 = {{27} \over 2}\sqrt 3 \cr} \)

Loigiaihay.com