Bài 34 trang 10 SBT Hình học 12 Nâng cao

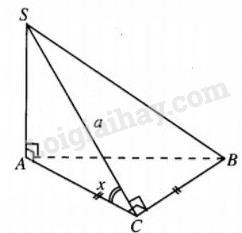
Đề bài

Khối chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh C và \(SA \bot \left( {ABC} \right),SC = a.\) Hãy tìm góc giữa hai mặt phẳng \(\left( {SCB} \right)\) và \(\left( {ABC} \right)\) để thể tích khối chóp là lớn nhất.

Lời giải chi tiết

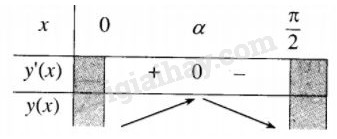
Ta có \(BC \bot AC\) nên \(BC \bot SC\) (định lý ba đường vuông góc), suy ra góc \(SCA\) là góc giữa hai mặt phẳng \(\left( {SCB} \right)\) và \(\left( {ABC} \right)\).

Đặt \(\widehat {SCA} = x\left( {0 < x < {\pi  \over 2}} \right)\)

Khi đó :

\(\eqalign{  & SA = a{\mathop{\rm s}\nolimits} {\rm{inx}},AC = acosx.  \cr  & {V_{S.ABC}} = {{a{\mathop{\rm s}\nolimits} {\rm{inx}}} \over 3}.{{{a^2}{\rm{co}}{{\rm{s}}^2}x} \over 2} = {{{a^3}} \over 6}{\mathop{\rm s}\nolimits} {\rm{in}x}.co{s^2}x. \cr} \)

Xét hàm số \(y\left( x \right) = \sin {\rm{x}}{\cos ^2}x.\)

Ta có :

\(\eqalign{  y'\left( x \right) &= co{s^3}x - 2{\mathop{\rm cosx}\nolimits} .s{\rm{i}}{{\rm{n}}^2}{\rm{x }}\cr&= \cos x\left( {co{s^2}x - 2 + 2co{s^2}x} \right)  \cr  &  = cosx\left( {3{{\cos }^2}x - 2} \right) \cr&= 3{\mathop{\rm cosx}\nolimits} \left( {{\mathop{\rm cosx}\nolimits}  - \sqrt {{2 \over 3}} } \right)\left( {\cos x + \sqrt {{2 \over 3}} } \right). \cr} \)

Vì \(0 < x < {\pi  \over 2}\) nên \(\cos x\left( {{\mathop{\rm cosx}\nolimits}  + \sqrt {{2 \over 3}} } \right) > 0.\)

Gọi \(\alpha \) là góc sao cho \(\cos \alpha  = \sqrt {{2 \over 3}} ,0 < \alpha  < {\pi  \over 2}.\)

Ta có bảng biến thiên của hàm \(y\left( x \right) = {\mathop{\rm s}\nolimits} {\rm{inx}}.{\cos ^2}x:\)

Vậy V_S.ABC đạt giá trị lớn nhất khi \(x = \alpha \) với \(0 < \alpha  < {\pi  \over 2}\) và \(\cos \alpha  = \sqrt {{2 \over 3}} .\)

Loigiaihay.com