Bài 3 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo

Đề bài

Cho hình chóp \(S.ABCD\) có các cạnh bên và cạnh đáy đều bằng \(a\). Gọi \(M\) là trung điểm của \({\rm{S}}A\). Mặt phẳng  \(\left( {MBD} \right)\) vuông góc với mặt phẳng nào dưới đây?

A. \(\left( {SBC} \right)\).

C. \(\left( {SBD} \right)\).

B. \(\left( {SAC} \right)\).

D. \(\left( {ABCD} \right)\).

Lời giải chi tiết

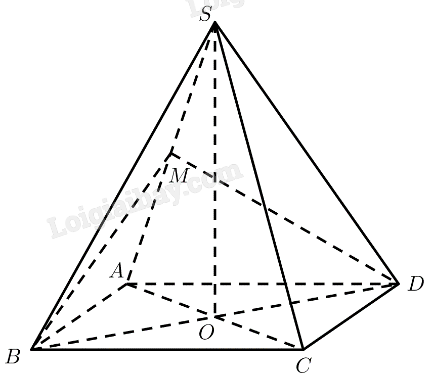
Gọi \(O\) là tâm của đáy \( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot B{\rm{D}}\)

\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)

\(\left. \begin{array}{l} \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\\B{\rm{D}} \subset \left( {MB{\rm{D}}} \right)\end{array} \right\} \Rightarrow \left( {MB{\rm{D}}} \right) \bot \left( {SAC} \right)\)

Chọn B.