Bài tập trắc nghiệm Toán 8 - Cánh diều

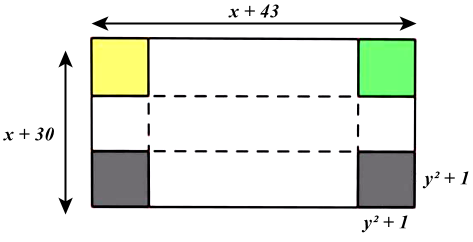
Trắc nghiệm Bài 2: Các phép tính với đa thức nhiều biến Toán 8 Cánh diều

Làm đề thi

Đề bài

Một tấm bìa cứng hình chữ nhật có chiều dài là x + 43 (cm), chiều rộng x+30 (cm). Người ta cắt ở mỗi góc của tấm bìa hình vuông cạnh \({y^2} + 1\) và xếp phần còn lại thành một cái hộp không nắp.

Câu 1

Tính chiều rộng của hình hộp chữ nhật.

  • A.

    \({x^2} - 2{y^2}(cm)\)

  • B.

    \(x - 2{y^2} + 28\left( {cm} \right)\)

  • C.

    \(x - {y^2}\left( {cm} \right)\)

  • D.

    \(x + 28\left( {cm} \right)\)

Câu 2

Tính chiều dài của hình hộp chữ nhật.

  • A.

    \(x + 2{y^2} + 41(cm)\)

  • B.

    \({x^2} + 2{y^2}\left( {cm} \right)\)

  • C.

    \(x - 2{y^2} + 41\left( {cm} \right)\)

  • D.

    \(x - 2{y^2}\left( {cm} \right)\)

Câu 3 :

Cho

\(\begin{array}{l}f\left( x \right) = {x^{2n}} - {x^{2n - 1}} + .... + {x^2} - x + 1\\g\left( x \right) =  - {x^{2n + 1}} + {x^{2n}} - {x^{2n - 1}} + .... + {x^2} - x + 1\end{array}\)

Biết \(h\left( x \right) = f\left( x \right) - g\left( x \right)\). Tính \(h\left( {\frac{1}{{10}}} \right)\)

  • A
    \(h\left( {\frac{1}{{10}}} \right) = \frac{{ - 1}}{{{{10}^{2n + 1}}}}\)
  • B
    \(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n + 1}}}}\)
  • C
    \(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n - 1}}}}\)
  • D
    \(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n - 1}}}}\)
Câu 4 :

Cho đa thức A = 3x – 1; B = 2y + 4x. Tính đa thức C = A + B khi x = 2y = 1.

  • A

    C = 8

  • B

    C = 7

  • C

    C = 9

  • D

    C = 10

Câu 5 :

Cho \(P = xyz + {x^2}{y^2}{z^2} + .... + {x^{2022}}{y^{2022}}{z^{2022}}\). Tính P biết: x = y = 1; z = -1.

  • A

    P = -2022

  • B

    P = 0

  • C

    P = 2022

  • D

    P = 1011

Câu 6 :

Một cửa hàng buổi sáng bán được: \(8{{{x}}^3}y + 5{{{x}}^6}{y^5} - 3{{{x}}^5}{y^4}\); buổi chiều bán được: \({x^6}{y^5} - {x^5}{y^4}\)(bao gạo). Tính số bao gạo mà của hàng bán được trong một ngày.

  • A
    \(8{{{x}}^3}y + 6{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)
  • B
    \(8{{{x}}^3}y + 6{{{x}}^6}{y^5}\)
  • C
    \(8{{{x}}^3}y + 5{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)
  • D
    \(6{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)
Câu 7 :

Khu vườn trồng mía của nhà bác Minh ban đầu có dạng hình vuông biết chu vi hình vuông là 20(m) sau đó mở rộng bên phải thêm y(m) phía dưới thêm 8x(m) nên mảnh vườn trở thành hình chữ nhật. Tính chu vi của khu vườn sau khi được mở rộng theo x, y

  • A

    y +5

  • B

    8x + 5

  • C

    2y +16x + 20

  • D

    4x + 8y

Câu 8 :

Bác Nam có một mảnh vườn hình chữ nhật có chiều dài là: \(2{y^2} + 12 + xy(m)\); chiều rộng là 2xy.(m). tính chu vi của khu vườn biết x = 4 và y = 4.

  • A
    184 m
  • B

    60m

  • C

    32m

  • D
    184\({m^2}\)
Câu 9 :

Nếu 3(4x + 5y) = P thì 12(12x+15y) bằng

  • A
    12P
  • B
    36P
  • C
    4P
  • D
    20P
Câu 10 :

Cho

\(\begin{array}{l}M = x - (y - z) - 2{{x}} + y + z - (2 - x - y)\\N = x - \left[ {x - \left( {y - 2{{z}}} \right) - 2{{z}}} \right]\end{array}\)

Tính M – N

  • A
    -2z + 2
  • B
    -2x – 2y – 2
  • C
    2z – 2
  • D
    -2x + 2y - 2
Câu 11 :

Tính giá trị của đa thức

\(N = {x^3} + {x^2}y - 2{{{x}}^2} - xy - {y^2} + 3y + x - 1\) biết x + y – 2 = 0

  • A
    -1
  • B
    0
  • C
    2
  • D
    1
Câu 12 :

Tính giá trị của đa thức

\(C = xy + {x^2}{y^2} + {x^3}{y^3} + ...... + {x^{100}}{y^{100}}.\)tại x = -1; y = -1

  • A
    -100
  • B
    100
  • C
    0
  • D
    50
Câu 13 :

Tìm đa thức M biết: \(M - \left( {{{3x}}y - 4{y^2}} \right) = {{{x}}^2}{{ - 7x}}y + 8{y^2}\)

  • A
    \(M = {x^2}{{ -  4x}}y + 4{y^2}\)
  • B
    \(M = {x^2}{{ + 4x}}y + 4{y^2}\)
  • C
    \(M =  - {x^2}{{ -  4x}}y + 4{y^2}\)
  • D
    \(M = {x^2} + 10{{x}}y + 4{y^2}\)
Câu 14 :

Tìm đa thức M biết \(M + \left( {5{{{x}}^2} - 2{{x}}y} \right) = 6{{{x}}^2} + 10{{x}}y - {y^2}\)

  • A
    \(M = {x^2} + 12{{x}}y - {y^2}\)
  • B
    \(M = {x^2} - 12{{x}}y - {y^2}\)
  • C
    \(M = {x^2} + 12{{x}}y + {y^2}\)
  • D
    \(M =  - {x^2} - 12{{x}}y - {y^2}\)
Câu 15 :

Cho đa thức

\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C =  - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)

Tính C – A – B:

  • A
    \(8{{{x}}^2} + 6{{x}}y + 2{y^2}\)
  • B
    \( - 8{{{x}}^2}{{ + 6x}}y - 2{y^2}\)
  • C
    \(8{{{x}}^2}{{ - 6x}}y - 2{y^2}\)
  • D
    \(8{{{x}}^2} - 6{{x}}y + 2{y^2}\)
Câu 16 :

Cho đa thức

\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C =  - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)

Tính A – B – C:

  • A
    \( - 10{{{x}}^2} + 2{{x}}y\)
  • B
    \( - 2{{{x}}^2} - 10{{x}}y\)
  • C
    \(2{{{x}}^2} + 10{{x}}y\)
  • D
    \(2{{{x}}^2} - 10{{x}}y\)
Câu 17 :

Cho các đa thức

\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C =  - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)

Tính A + B +C:

  • A
    \(7{{{x}}^2} + 6{y^2}\)
  • B
    \(5{{{x}}^2} + 5{y^2}\)
  • C
    \(6{{{x}}^2} + 6{y^2}\)
  • D
    \(6{{{x}}^2} - 6{y^2}\)
Câu 18 :

Tính \(\left( {xy + {y^2} - {x^2}{y^2} - 2} \right) + \left( {{x^2}{y^2} + 5 - {y^2}} \right)\)

  • A
    xy + 3
  • B
    xy – 3
  • C
    –xy + 3
  • D
    –xy - 3
Câu 19 :

Cho \(f(x) = 3{{{x}}^4} + 2{{{x}}^3} - 2{{{x}}^4} + {x^2} - 5{{x}} + 6\)

Tính \(f( - 1)\)

  • A
    8
  • B
    9
  • C
    11
  • D
    10
Câu 20 :

Cho các đa thức:

\(\begin{array}{l}M = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 2\\P = 3{{{x}}^3} - 2{{{x}}^2}y - xy + 3\end{array}\)

Tính M – P

  • A
    \({x^2}y + 3{{x}}y + 1\)
  • B
    \({x^2}y - 3{{x}}y - 1\)
  • C
    \( - {x^2}y + 3{{x}}y - 1\)
  • D
    \({x^2}y + 3{{x}}y - 1\)
Câu 21 :

Cho các đa thức:

\(\begin{array}{l}M = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 3\\N = {x^2}y - 2{{x}}y - 2\end{array}\)

Tính M + 2N

  • A
    \(3{{{x}}^3} - 1\)               
  • B
    \(3{{{x}}^3} + {x^2}y - 2{{x}}y + 1\)
  • C
    \(3{{{x}}^3} - {x^2}y + 2{{x}}y - 1\)
  • D
    \(3{{{x}}^3} + {x^2}y - 2{{x}}y - 1\)
Câu 22 :

Xác định ba số tự nhiên liên tiếp biết tích hai số đầu nhỏ hơn tích giữa số đầu và số cuối là \(9\).

  • A
    \(9;10;11\).
  • B
    \(8;9;10\).
  • C
    \(10;11;12\).
  • D
    \(7;8;9\).
Câu 23 :

Giá trị biểu thức \({x^4} - 2022{x^3} + 2022{x^2} - 2022x + 2022\) tại \(x = 2021\)là

  • A
    \(2022\).
  • B
    \(2021\).
  • C
    \(1\).
  • D
    \( - 1\).
Câu 24 :

Cho m số mà mỗi số bằng 3n – 1 và n số mà mỗi số bằng 9 – 3m. Biết tổng tất cả các số đó bằng 5 lần tổng m + n. Khi đó:

  • A
    \(m = \frac{2}{3}n\)
  • B
    \(m = n\)
  • C
    \(m = 2n\)
  • D
    \(m = \frac{3}{2}n\)
Câu 25 :

Cho B = (m – 1)(m + 6) – (m + 1)(m – 6). Chọn kết luận đúng.

  • A
    B ⁝ 10 với mọi m Є Z          
  • B
    B ⁝ 15 với mọi m Є Z 
  • C
    B ⁝ 9 với mọi m Є Z            
  • D
    B ⁝ 20 với mọi m Є Z 
Câu 26 :

Cho x2 + y2 = 2, đẳng thức nào sau đây đúng?

  • A
    2(x + 1)(y + 1) = (x + y)(x + y – 2)                    
  • B
    2(x + 1)(y + 1) = (x + y)(x + y + 2)
  • C
    2(x + 1)(y + 1) =  x + y                   
  • D
    (x + 1)(y + 1) = (x + y)(x + y + 2)
Câu 27 :

Gọi x là giá trị thỏa mãn

(3x – 4)(x – 2) = 3x(x – 9) – 3. Khi đó

  • A
    x < 0                 
  • B
    x < -1                
  • C
    x > 2                 
  • D
    x > 0
Câu 28 :

Kết quả rút gọn biểu thức  \(3x\left( {x - 5y} \right) + \left( {y - 5x} \right)\left( { - 3y} \right) - 3\left( {{x^2} - {y^2}} \right) - 1\) là

  • A
    \(3\).
  • B

    \(0\).

  • C

    \( - 1\). 

  • D

    \(1\).

Câu 29 :

Giá trị \(x\), thỏa mãn \(3x\left( {12x - 4} \right) - 9x\left( {4x - 3} \right) = 30\) là

  • A
    \(0\).
  • B
    \(3\).
  • C
    \(1\).
  • D
    \(2\).
Câu 30 :

Rút gọn biểu thức \(\left( {3x - 5} \right)\left( {2x + 11} \right) - \left( {2x + 3} \right)\left( {3x + 7} \right)\). Khẳng định nào sau đây là đúng?

  • A
    \(6{x^2} - 15x + 55\).
  • B
    Không phụ thuộc vào giá trị của biến \(x\).
  • C
    \( - 43x - 55\).
  • D
    76.
Câu 31 :

Giá trị \(m\) thỏa mãn \(\left( {{x^2} - x + 1} \right)x - \left( {x + 1} \right){x^2} + m - 5 =  - 2{x^2} + x\) là

  • A
    \( - 5\).
  • B
    \(5\).
  • C
    \(4\).
  • D
    \(15\).
Câu 32 :

Hệ số của \({x^3}\) và \({x^2}\)trong đa thức \(B = \left( {{x^3} - 3{x^2} + 2x + 1} \right)\left( { - {x^2}} \right) - x\left( {2{x^2} - 3x + 1} \right)\) là

  • A
    \( - 4;2\).
  • B
    \(4; - 2\).
  • C
    \(2;4\).
  • D
    \( - 4; - 2\).
Câu 33 :

Giá trị của biểu thức \({x^2}\left( {x + y} \right) - y\left( {{x^2} - {y^2}} \right)\) tại \(x =  - 1;y = 10\) là:

  • A
    \( - 1001\).
  • B
    \(1001\).
  • C
    \(999\).
  • D
    \( - 999\).
Câu 34 :

Thực hiện phép tính nhân \(\left( {x - 1} \right)\left( {x + 3} \right)\) ta được kết quả

  • A
    \({x^2} - 3\).
  • B
    \({x^2} + 3\).
  • C
    \({x^2} + 2x - 3\).
  • D
    \({x^2} - 4x + 3\).
Câu 35 :

Giá trị của \(a\), \(b\), \(c\) biết \(\left( {a{x^2} + bx + c} \right)\left( {x + 3} \right) = {x^3} + 2{x^2} - 3x\) là

  • A

    \(a = 1\), \(b = 1\), \(c = 0\).

  • B

    \(a = 2\), \(b = 1\), \(c = 1\).

  • C

    \(a = 1\), \(b =  - 1\), \(c = 0\).

  • D

    \(a =  - 1\), \(b = 2\), \(c = 1\).

Câu 36 :

Thực hiện phép tính nhân \(x\left( {2{x^2} + 1} \right)\) ta được kết quả:

  • A
    \(3{x^2} + x\).
  • B
    \(3{x^3} + x\).
  • C
    \(2{x^3} + x\).
  • D
    \(2{x^3} + 1\).
Câu 37 :

Với giá trị tự nhiên nào của \(n\) thì phép chia \(\left( {14{x^8}{y^4} - 9{x^{2n}}{y^6}} \right):\left( { - 2{x^7}{y^n}} \right)\) là phép chia hết?

  • A

    \(\frac{7}{2} \le n \le 4\).

  • B

    \(n = 4\).

  • C

    \(n \ge \frac{7}{2}\).

  • D

    \(n \ge 4\).

Câu 38 :

Cho \(P = \left( {75{x^5}{y^2} - 45{x^4}{y^3}} \right):\left( {3{x^3}{y^2}} \right) - \left( {\frac{5}{2}{x^2}{y^4} - 2x{y^5}} \right):\left( {\frac{1}{2}x{y^3}} \right)\). Khẳng định nào sai?

  • A

    \(P \ge 0,\,\,\forall x,\,\,y \ne 0\).

  • B

    \(P > 0 \Leftrightarrow 5x - 2y \ne 0\).

  • C

    \(P = 0 \Leftrightarrow 5x = 2y \ne 0\).

  • D

    \(P\) nhận cả giá trị âm và dương.

Câu 39 :

Một cửa hàng buổi sáng bán được xy bao gạo thì của hàng đó thu được số tiền là \({x^6}{y^5} - {x^5}{y^4}\) nghìn đồng. Tính số tiền mỗi bao gạo của cửa hàng đó đã bán khi x = 2; y = 2.

  • A

    384 nghìn đồng                         

  • B

    284 nghìn đồng

  • C

    120 nghìn đồng                         

  • D

    84 nghìn đồng

Câu 40 :

Tìm đơn thức B biết: \(\left( {B + 2{x^2}{y^3}} \right).\left( { - 3xy} \right) =  - 3{x^2}{y^2} - 6{x^3}{y^4}\)

  • A

    \(B = xy\)                   

  • B

    \(B =  - xy\)                       

  • C

    \(B = x + 1\)                 

  • D

    \(B = {x^2}y\)

Câu 41 :

Chọn kết luận đúng về biểu thức:

\(E = \frac{2}{3}{x^2}{y^3}:\left( {\frac{{ - 1}}{3}xy} \right) + 2x\left( {y - 1} \right)\left( {y + 1} \right)\left( {x \ne 0;y \ne 0;y \ne 1} \right)\)

  • A

    Giá trị của biểu thức không phụ thuộc vào biến x.

  • B

    Giá trị của biểu thức không phụ thuộc vào biến y.

  • C

    Giá trị của biểu thức không phụ thuộc vào biến.

  • D

    Giá trị của biểu thức bằng 0.

Câu 42 :

Giá trị của số tự nhiên thỏa mãn điều kiện gì để phép chia \({x^{n + 3}}{y^6}:{x^9}{y^n}\) là phép chia hết?

  • A

    n < 6

  • B

    n = 5

  • C

    n > 6

  • D

    n = 6

Câu 43 :

Giá trị của biểu thức: \(A = \left[ {{{\left( {x - y} \right)}^5} + {{\left( {x - y} \right)}^4} + {{\left( {x - y} \right)}^3}} \right]:\left( {x - y} \right)\) với x= 3; y = 1 là:

  • A

    28

  • B

    16

  • C

    20

  • D

    14

Câu 44 :

Tính giá trị của biểu thức

D = \(\left( {15x{y^2}\; + {{ }}18x{y^3}\; + {{ }}16{y^2}} \right){{ }}:{{ }}6{y^2}\;-{{ }}7{x^4}{y^3}\;:{{ }}{x^4}y\) tại \(x = \frac{2}{3}{;^{}}y = 1\) là:

  • A

    \(\frac{{28}}{3}\) 

  • B

    \(\frac{3}{2}\)

  • C

    \(\frac{2}{3}\)

  • D

    \( - \frac{2}{3}\)

Câu 45 :

Biểu thức \(D = \left( {9{x^2}{y^2} - 6{x^2}{y^3}} \right):{( - 3xy)^2} + \left( {6{x^5}y + 2{x^4}} \right):\left( {2{x^4}} \right)\) sau khi rút gọn là một đa thức có bậc bằng

  • A

    1.

  • B

    2.

  • C

    3.

  • D

    4.

Câu 46 :

Tất cả các giá trị của \(x\) để \(\left( {2{x^4} - 3{x^3} + {x^2}} \right):\left( { - {x^2}} \right) + 4{(x - 1)^2} = 0\) là

  • A

    \(x \in \left\{ {1;\frac{3}{2}} \right\}\).

  • B

    \(x \in \left\{ { - 1;\frac{3}{2}} \right\}\).

  • C

    \(x \in \left\{ {1; - \frac{3}{2}} \right\}\).

  • D

    \(x \in \left\{ { - 1; - \frac{3}{2}} \right\}\).

Câu 47 :

Đa thức \(N\) thỏa mãn \( - 15{x^6}{y^5} - 20{x^4}{y^4} - 25{x^5}{y^3} = \left( { - 5{x^3}{y^2}} \right)N\) là

  • A

    \(N =  - 3{x^3}{y^3} + 4x{y^2} + 5{x^2}y\).

  • B

    \(N =  - 3{x^2}{y^3} + 4xy + 5{x^2}y\).

  • C

    \(N = 3{x^3}{y^3} + 4x{y^2} + 5{x^2}y\).

  • D

    \(N = 3{x^3}{y^3} + 4x{y^2} + 5xy\).

Câu 48 :

Giá trị của biểu thức \(P = \left[ {{{(3ab)}^2} - 9{a^2}{b^4}} \right]:\left( {8a{b^2}} \right)\) tại \(a = \frac{2}{3};b = \frac{3}{2}\) là

  • A

    \(\frac{{ - 23}}{{16}}\).

  • B

    \(\frac{{ - 25}}{8}\).

  • C

    \(\frac{{ - 15}}{{16}}\).

  • D

    \(\frac{{ - 21}}{8}\).

Câu 49 :

Kết quả phép tính \(\left( {7{x^4} - 3{x^5} + 2{x^2}} \right):\left( {\frac{3}{4}{x^2}} \right)\) là một đa thức có hệ số cao nhất bằng

  • A

    \(\frac{{28}}{3}\).

  • B

    -4.

  • C

    \(\frac{8}{3}\).

  • D

    -3.

Câu 50 :

Đa thức \(7{x^3}{y^2}z - 2{x^4}{y^3}\) chia hết cho đơn thức nào dưới đây?

  • A

    \(3{x^4}\).

  • B

    \( - 3{x^4}\).

  • C

    \( - 2{x^3}y\).

  • D

    \(2x{y^3}\).

Câu 51 :

Thực hiện phép chia \(\left( {2{x^4}y - 6{x^2}{y^7}} \right):\left( {2{x^2}} \right)\) ta được đa thức \(a{x^2}y + b{y^7}(a,b\) là hằng số). Khi đó \(a + b\) bằng

  • A

    -3.

  • B

    -4.

  • C

    -2.

  • D

    -5.

Câu 52 :

Kết quả phép chia \(\left( {6{x^4}y + 4{x^3}{y^3} - 2xy} \right):(xy)\) là một đa thức có bậc bằng

  • A

    3.

  • B

    4.

  • C

    7.

  • D

    9.

Câu 53 :

Kết quả của phép chia \(\left[ {{{(x - y)}^3} - {{(x - y)}^2} + (x - y)} \right]:(y - x)\) là

  • A

    \({(x - y)^2} - (x - y) + 1\).

  • B

    \( - {(x - y)^2} + (x - y) + 1\).

  • C

    \({(x - y)^2} + (x - y) + 1\).

  • D

    \( - {(x - y)^2} + (x - y) - 1\).

Câu 54 :

Kết quả của phép chia \(\left( {3{x^3} + 2{x^2} + x} \right):(3x)\) là một đa thức có hệ số tự do là

  • A

    1.

  • B

    \(\frac{2}{3}\).

  • C

    \(\frac{1}{3}\).

  • D

    0.

Câu 55 :

Kết quả phép chia \(\left( {2{x^3} + 3{x^4} - 12{x^2}} \right):x\) là

  • A

    \(2{x^2} + 3{x^4} - 12{x^2}\).

  • B

    \(2{x^2} + 3{x^3} - 12{x^2}\).

  • C

    \(2{x^2} + 3{x^4} - 12x\).

  • D

    \(2{x^2} + 3{x^3} - 12x\).

Lời giải và đáp án

Một tấm bìa cứng hình chữ nhật có chiều dài là x + 43 (cm), chiều rộng x+30 (cm). Người ta cắt ở mỗi góc của tấm bìa hình vuông cạnh \({y^2} + 1\) và xếp phần còn lại thành một cái hộp không nắp.

Câu 1

Tính chiều rộng của hình hộp chữ nhật.

  • A.

    \({x^2} - 2{y^2}(cm)\)

  • B.

    \(x - 2{y^2} + 28\left( {cm} \right)\)

  • C.

    \(x - {y^2}\left( {cm} \right)\)

  • D.

    \(x + 28\left( {cm} \right)\)

Đáp án : B

Phương pháp giải :

Chiều rộng của hình hộp chữ nhật bằng chiều rộng ban đầu trừ đi hai lần cạnh của hình vuông.

Lời giải chi tiết :

Chiều rộng của hình hộp chữ nhật là:

\(\left( {x + 30} \right) - \left( {{y^2} + 1} \right).2 = x - 2{y^2} + 28(cm)\)

Câu 2

Tính chiều dài của hình hộp chữ nhật.

  • A.

    \(x + 2{y^2} + 41(cm)\)

  • B.

    \({x^2} + 2{y^2}\left( {cm} \right)\)

  • C.

    \(x - 2{y^2} + 41\left( {cm} \right)\)

  • D.

    \(x - 2{y^2}\left( {cm} \right)\)

Đáp án : C

Phương pháp giải :

Chiều dài của hình hộp chữ nhật bằng chiều dài ban đầu trừ đi hai lần cạnh của hình vuông

Lời giải chi tiết :

Chiều dài của hình hộp chữ nhật là:

\(\left( {x + 43} \right) - \left( {{y^2} + 1} \right).2 = x - 2{y^2} + 41(cm)\)

Câu 3 :

Cho

\(\begin{array}{l}f\left( x \right) = {x^{2n}} - {x^{2n - 1}} + .... + {x^2} - x + 1\\g\left( x \right) =  - {x^{2n + 1}} + {x^{2n}} - {x^{2n - 1}} + .... + {x^2} - x + 1\end{array}\)

Biết \(h\left( x \right) = f\left( x \right) - g\left( x \right)\). Tính \(h\left( {\frac{1}{{10}}} \right)\)

  • A
    \(h\left( {\frac{1}{{10}}} \right) = \frac{{ - 1}}{{{{10}^{2n + 1}}}}\)
  • B
    \(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n + 1}}}}\)
  • C
    \(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n - 1}}}}\)
  • D
    \(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n - 1}}}}\)

Đáp án : B

Phương pháp giải :
Tính h(x) = f(x) – g(x)

Thay \(x = \frac{1}{{10}}\)vào h(x)

Lời giải chi tiết :
Ta có:

\(\begin{array}{l}h\left( x \right) = f\left( x \right) - g\left( x \right)\\ = \left( {{x^{2n}} - {x^{2n - 1}} + ..... + {x^2} - x + 1} \right) - \left( { - {x^{2n + 1}} + {x^{2n}} - {x^{2n - 1}} + .... + {x^2} - x + 1} \right)\\ = {x^{2n}} - {x^{2n - 1}} + ..... + {x^2} - x + 1 + {x^{2n + 1}} - {x^{2n}} + {x^{2n + 1}} - .... - {x^2} + x - 1\\ = {x^{2n + 1}} + \left( {{x^{2n}} - {x^{2n}}} \right) + \left( { - {x^{2n - 1}} + {x^{2n - 1}}} \right) + .... + \left( {{x^2} - {x^2}} \right) + \left( { - x + x} \right) + \left( {1 - 1} \right)\\ = {x^{2n + 1}}\end{array}\)

Thay \(x = \frac{1}{{10}}\)vào h(x) ta được:

\(h\left( {\frac{1}{{10}}} \right) = {\left( {\frac{1}{{10}}} \right)^{2n + 1}} = \frac{1}{{{{10}^{2n + 1}}}}\)

Câu 4 :

Cho đa thức A = 3x – 1; B = 2y + 4x. Tính đa thức C = A + B khi x = 2y = 1.

  • A

    C = 8

  • B

    C = 7

  • C

    C = 9

  • D

    C = 10

Đáp án : B

Phương pháp giải :
Từ x = 2y = 1 tìm ra x, y thay vào C = A + B.
Lời giải chi tiết :

Ta có: C = A + B = 3x – 1 +2y +4x = 7x + 2y - 1 với

\(x = 2y = 1 \Rightarrow \left\{ \begin{array}{l}x = 1\\2y = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 1\\y = \frac{1}{2}\end{array} \right.\) Thay  \(x = 1;y = \frac{1}{2}\)vào C ta được:

\(C = 7.1 + 2.\frac{1}{2} - 1 = 7 + 1 - 1 = 7\)

Câu 5 :

Cho \(P = xyz + {x^2}{y^2}{z^2} + .... + {x^{2022}}{y^{2022}}{z^{2022}}\). Tính P biết: x = y = 1; z = -1.

  • A

    P = -2022

  • B

    P = 0

  • C

    P = 2022

  • D

    P = 1011

Đáp án : B

Phương pháp giải :
Thay x = y = 1; z = -1 vào P.
Lời giải chi tiết :
Thay x = y =1; z = -1 và P ta được

\(\begin{array}{l}P = 1.1\left( { - 1} \right) + {1^2}{.1^2}{\left( { - 1} \right)^2} + .... + {1^{2022}}{.1^{2022}}{\left( { - 1} \right)^{2022}}\\ = \left( { - 1} \right) + 1 + \left( { - 1} \right) + .... + \left( { - 1} \right) = 0\end{array}\)

Câu 6 :

Một cửa hàng buổi sáng bán được: \(8{{{x}}^3}y + 5{{{x}}^6}{y^5} - 3{{{x}}^5}{y^4}\); buổi chiều bán được: \({x^6}{y^5} - {x^5}{y^4}\)(bao gạo). Tính số bao gạo mà của hàng bán được trong một ngày.

  • A
    \(8{{{x}}^3}y + 6{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)
  • B
    \(8{{{x}}^3}y + 6{{{x}}^6}{y^5}\)
  • C
    \(8{{{x}}^3}y + 5{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)
  • D
    \(6{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)

Đáp án : A

Phương pháp giải :

Cộng số bao gạo bán được của buổi sáng và buổi chiều rồi rút gọn.

Lời giải chi tiết :
Số bao gạo của hàng bán được trong một ngày là:

\(\begin{array}{l}\left( {8{{{x}}^3}y + 5{{{x}}^6}{y^5} - 3{{{x}}^5}{y^4}} \right) + \left( {{x^6}{y^5} - {x^5}{y^4}} \right)\\ = 8{{{x}}^3}y + 6{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\end{array}\)

Câu 7 :

Khu vườn trồng mía của nhà bác Minh ban đầu có dạng hình vuông biết chu vi hình vuông là 20(m) sau đó mở rộng bên phải thêm y(m) phía dưới thêm 8x(m) nên mảnh vườn trở thành hình chữ nhật. Tính chu vi của khu vườn sau khi được mở rộng theo x, y

  • A

    y +5

  • B

    8x + 5

  • C

    2y +16x + 20

  • D

    4x + 8y

Đáp án : C

Phương pháp giải :

Xác định chiều dài, chiều rộng của khu vườn sau khi được mở rộng. Tính chu vi của khu vườn sau khi mở rộng

Lời giải chi tiết :
Cạnh của mảnh vườn hình vuông ban đầu là: 20 : 4 = 5(m)

Chiều rộng của khu vườn sau khi được mở rộng là: y +5 (m)

Chiều dài của khu vườn sau khi được mở rộng là: 8x + 5 (m)

Chu vi của khu vườn là: 2(y + 5 + 8x + 5) = 2.(y + 8x + 10) = 2y + 16x + 20 (m)

Câu 8 :

Bác Nam có một mảnh vườn hình chữ nhật có chiều dài là: \(2{y^2} + 12 + xy(m)\); chiều rộng là 2xy.(m). tính chu vi của khu vườn biết x = 4 và y = 4.

  • A
    184 m
  • B

    60m

  • C

    32m

  • D
    184\({m^2}\)

Đáp án : A

Phương pháp giải :
Viết công thức tính chu vi của khu vườn. Thay x = 4; y = 4 vào công thức chu vi của khu vườn
Lời giải chi tiết :
Chu vi của khu vườn là:

\(2.\left( {2{y^2} + 12 + xy + 2{{x}}y} \right) = 2.\left( {2{y^2} + 12 + 3{{x}}y} \right) = 4{y^2} + 24 + 6{{x}}y\)

Thay x = 4; y = 4 vào công thức chu vi ta được:

\({4.4^2} + 24 + 6.4.4 = 184m\)

Câu 9 :

Nếu 3(4x + 5y) = P thì 12(12x+15y) bằng

  • A
    12P
  • B
    36P
  • C
    4P
  • D
    20P

Đáp án : A

Phương pháp giải :
Biến đổi 12(12x + 15y) thành tích có chứa thừa số 3(4x +5y)
Lời giải chi tiết :
Ta có:

12(12x +15y) = 12(3.4x + 3.5y) = 12.3(4x +5y) = 12P

Câu 10 :

Cho

\(\begin{array}{l}M = x - (y - z) - 2{{x}} + y + z - (2 - x - y)\\N = x - \left[ {x - \left( {y - 2{{z}}} \right) - 2{{z}}} \right]\end{array}\)

Tính M – N

  • A
    -2z + 2
  • B
    -2x – 2y – 2
  • C
    2z – 2
  • D
    -2x + 2y - 2

Đáp án : C

Phương pháp giải :
Rút gọn M, N rồi tính M - N
Lời giải chi tiết :
Ta có:

\(\begin{array}{l}M = x - \left( {y - z} \right) - 2{{x}} + y + z - \left( {2 - x - y} \right)\\ = x - y + z - 2{{x}} + y + z - 2 + x + y\\ = y + 2{{z}} - 2\\N = x - \left[ {x - \left( {y - 2{{z}}} \right) - 2{{z}}} \right]\\ = x - \left( {x - y + 2{{z}} - 2{{z}}} \right) = x - x + y = y\\ \Rightarrow M - N = y + 2{{z}} - 2 - y = 2{{z}} - 2\end{array}\)

Câu 11 :

Tính giá trị của đa thức

\(N = {x^3} + {x^2}y - 2{{{x}}^2} - xy - {y^2} + 3y + x - 1\) biết x + y – 2 = 0

  • A
    -1
  • B
    0
  • C
    2
  • D
    1

Đáp án : D

Phương pháp giải :
Nhóm các hạng tử của đa thức để biến đổi thành x + y – 2 = 0
Lời giải chi tiết :
Ta có:

\(\begin{array}{l}N = {x^3} + {x^2}y - 2{{{x}}^2} - xy - {y^2} + 3y + x - 1\\ = \left( {{x^3} + {x^2}y - 2{{{x}}^2}} \right) + \left( { - xy - {y^2} + 2y} \right) + y + x - 1\\ = {x^2}\left( {x + y - 2} \right) - y\left( {x + y - 2} \right) + \left( {x + y - 2} \right) + 1\\ = {x^2}.0 - y.0 + 0 + 1 = 1\end{array}\)

Câu 12 :

Tính giá trị của đa thức

\(C = xy + {x^2}{y^2} + {x^3}{y^3} + ...... + {x^{100}}{y^{100}}.\)tại x = -1; y = -1

  • A
    -100
  • B
    100
  • C
    0
  • D
    50

Đáp án : B

Phương pháp giải :
Thay x = -1; y = -1 vào đa thức C ta được giá trị của C.
Lời giải chi tiết :
Thay x = -1; y = -1 vào đa thức C ta được.

\(\begin{array}{l}C = ( - 1)\left( { - 1} \right) + {\left( { - 1} \right)^2}{\left( { - 1} \right)^2} + {\left( { - 1} \right)^3}{\left( { - 1} \right)^3} + ........... + {\left( { - 1} \right)^{100}}{\left( { - 1} \right)^{100}}\\C = 1 + 1 + 1 + ..... + 1 = 100\end{array}\)

Câu 13 :

Tìm đa thức M biết: \(M - \left( {{{3x}}y - 4{y^2}} \right) = {{{x}}^2}{{ - 7x}}y + 8{y^2}\)

  • A
    \(M = {x^2}{{ -  4x}}y + 4{y^2}\)
  • B
    \(M = {x^2}{{ + 4x}}y + 4{y^2}\)
  • C
    \(M =  - {x^2}{{ -  4x}}y + 4{y^2}\)
  • D
    \(M = {x^2} + 10{{x}}y + 4{y^2}\)

Đáp án : A

Phương pháp giải :
Áp dụng \(M - A = B \Rightarrow M = B + A\)
Lời giải chi tiết :
Ta có:

\(\begin{array}{l}M - \left( {{{3x}}y - 4{y^2}} \right) = {{{x}}^2}{{ - 7x}}y + 8{y^2}\\ \Rightarrow M = {x^2} - 7{{x}}y + 8{y^2} + \left( {3{{x}}y - 4{y^2}} \right)\\M = {x^2} + \left( { - 7{{x}}y + 3{{x}}y} \right) + \left( {8{y^2} - 4{y^2}} \right)\\ \Rightarrow M = {x^2} - 4{{x}}y + 4{y^2}\end{array}\)

Câu 14 :

Tìm đa thức M biết \(M + \left( {5{{{x}}^2} - 2{{x}}y} \right) = 6{{{x}}^2} + 10{{x}}y - {y^2}\)

  • A
    \(M = {x^2} + 12{{x}}y - {y^2}\)
  • B
    \(M = {x^2} - 12{{x}}y - {y^2}\)
  • C
    \(M = {x^2} + 12{{x}}y + {y^2}\)
  • D
    \(M =  - {x^2} - 12{{x}}y - {y^2}\)

Đáp án : A

Phương pháp giải :
Áp dụng: \(M + A = B \Rightarrow M = B - A\)
Lời giải chi tiết :
Ta có:

\(\begin{array}{l}M + \left( {5{{{x}}^2} - 2{{x}}y} \right) = 6{{{x}}^2} + 10{{x}}y - {y^2}\\ \Rightarrow M = 6{{{x}}^2} + 10{{x}}y - {y^2} - \left( {5{{{x}}^2} - 2{{xy}}} \right)\\M = \left( {6{{{x}}^2} - 5{{{x}}^2}} \right) + \left( {10{{x}}y + 2{{x}}y} \right) - {y^2}\\ \Rightarrow M = {x^2} + 12{{x}}y - {y^2}\end{array}\)

Câu 15 :

Cho đa thức

\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C =  - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)

Tính C – A – B:

  • A
    \(8{{{x}}^2} + 6{{x}}y + 2{y^2}\)
  • B
    \( - 8{{{x}}^2}{{ + 6x}}y - 2{y^2}\)
  • C
    \(8{{{x}}^2}{{ - 6x}}y - 2{y^2}\)
  • D
    \(8{{{x}}^2} - 6{{x}}y + 2{y^2}\)

Đáp án : B

Phương pháp giải :
Áp dụng quy tắc trừ các đa thức
Lời giải chi tiết :

\(\begin{array}{l}C - A - B = \left( { - {x^2} + 3{{x}}y + 2{y^2}} \right) - \left( {4{{{x}}^2} - 5{{x}}y + 3{y^2}} \right) - \left( {3{{{x}}^2} + 2{{x}}y + {y^2}} \right) \\ = - {x^2} + 3{{x}}y + 2{y^2} - 4{{{x}}^2} + 5{{x}}y - 3{y^2} - 3{{{x}}^2} - 2{{x}}y - {y^2} \\ = \left( { - 4{{{x}}^2} - 3{{{x}}^2} - {x^2}} \right) + \left( {5{{x}}y - 2{{x}}y + 3{{x}}y} \right) + \left( { - 3{y^2} - {y^2} + 2{y^2}} \right)\\ =  - 8{{{x}}^2}{{ + 6x}}y - 2{y^2}\end{array}\)

Câu 16 :

Cho đa thức

\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C =  - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)

Tính A – B – C:

  • A
    \( - 10{{{x}}^2} + 2{{x}}y\)
  • B
    \( - 2{{{x}}^2} - 10{{x}}y\)
  • C
    \(2{{{x}}^2} + 10{{x}}y\)
  • D
    \(2{{{x}}^2} - 10{{x}}y\)

Đáp án : D

Phương pháp giải :
Áp dụng quy tắc trừ các đa thức.
Lời giải chi tiết :
Ta có:

\(\begin{array}{l}A - B - C = \left( {4{{{x}}^2} - 5{{x}}y + 3{y^2}} \right) - \left( {3{{{x}}^2} + 2{{x}}y + {y^2}} \right) - \left( { - {x^2} + 3{{x}}y + 2{y^2}} \right)\\ = 4{{{x}}^2} - 5{{x}}y + 3{y^2} - 3{{{x}}^2} - 2{{x}}y - {y^2} + {x^2} - 3{{x}}y - 2{y^2}\\ = \left( {4{{{x}}^2} - 3{{{x}}^2} + {x^2}} \right) + \left( { - 5{{x}}y - 2{{x}}y - 3{{x}}y} \right) + \left( {3{y^2} - {y^2} - 2{y^2}} \right)\\ = 2{{{x}}^2} - 10{{x}}y\end{array}\)

Câu 17 :

Cho các đa thức

\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C =  - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)

Tính A + B +C:

  • A
    \(7{{{x}}^2} + 6{y^2}\)
  • B
    \(5{{{x}}^2} + 5{y^2}\)
  • C
    \(6{{{x}}^2} + 6{y^2}\)
  • D
    \(6{{{x}}^2} - 6{y^2}\)

Đáp án : C

Phương pháp giải :
Áp dụng quy tắc cộng các đa thức
Lời giải chi tiết :
Ta có:

\(\begin{array}{l}A + B + C = (4{{{x}}^2} - 5{{x}}y + 3{y^2}) + (3{{{x}}^2} + 2{{x}}y + {y^2}) + ( - {x^2} + 3{{x}}y + 2{y^2})\\ = 4{{{x}}^2} - 5{{x}}y + 3{y^2} + 3{{{x}}^2} + 2{{x}}y + {y^2} - {x^2} + 3{{x}}y + 2{y^2}\\ = \left( {4{{{x}}^2} + 3{{{x}}^2} - {x^2}} \right) + \left( { - 5{{x}}y + 2{{x}}y + 3{{x}}y} \right) + \left( {3{y^2} + {y^2} + 2{y^2}} \right)\\ = 6{{{x}}^2} + 6{y^2}\end{array}\)

Câu 18 :

Tính \(\left( {xy + {y^2} - {x^2}{y^2} - 2} \right) + \left( {{x^2}{y^2} + 5 - {y^2}} \right)\)

  • A
    xy + 3
  • B
    xy – 3
  • C
    –xy + 3
  • D
    –xy - 3

Đáp án : A

Phương pháp giải :
Áp dụng quy tắc tính tổng 2 đa thức
Lời giải chi tiết :
Ta có:

\(\begin{array}{l}\left( {xy + {y^2} - {x^2}{y^2} - 2} \right) + \left( {{x^2}{y^2} + 5 - {y^2}} \right)\\ = xy + {y^2} - {x^2}{y^2} - 2 + {x^2}{y^2} + 5 - {y^2}\\ = \left( { - {x^2}{y^2} + {x^2}{y^2}} \right) + xy + \left( {{y^2} - {y^2}} \right) + \left( { - 2 + 5} \right)\\ = xy + 3\end{array}\)

Câu 19 :

Cho \(f(x) = 3{{{x}}^4} + 2{{{x}}^3} - 2{{{x}}^4} + {x^2} - 5{{x}} + 6\)

Tính \(f( - 1)\)

  • A
    8
  • B
    9
  • C
    11
  • D
    10

Đáp án : C

Phương pháp giải :

Thu gọn đa thức theo quy tắc cộng trừ đa thức

Thay x = -1 vào đa thức f(x) thu gọn

Lời giải chi tiết :

Ta có: \(\begin{array}{l}f(x) = 3{{{x}}^4} + 2{{{x}}^3} - 2{{{x}}^4} + {x^2} - 5{{x}} + 6\\ = (3{x^4} - 2{{x}}{}^4) + 2{{{x}}^3} + {x^2} - 5{{x}} + 6\\ = {x^4} + 2{{{x}}^3} + {x^2} - 5{{x}} + 6\end{array}\)

Sau đó thay x = -1 vào đa thức \(f\left( x \right)\)thu gọn ta được

\(f\left( { - 1} \right) = {\left( { - 1} \right)^4} + 2{\left( { - 1} \right)^3} + {\left( { - 1} \right)^2} - 5\left( { - 1} \right) + 6 = 11\)

Câu 20 :

Cho các đa thức:

\(\begin{array}{l}M = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 2\\P = 3{{{x}}^3} - 2{{{x}}^2}y - xy + 3\end{array}\)

Tính M – P

  • A
    \({x^2}y + 3{{x}}y + 1\)
  • B
    \({x^2}y - 3{{x}}y - 1\)
  • C
    \( - {x^2}y + 3{{x}}y - 1\)
  • D
    \({x^2}y + 3{{x}}y - 1\)

Đáp án : D

Phương pháp giải :

Tính M – P  và nhóm các đơn thức đồng dạng.

 

Lời giải chi tiết :

\(\begin{array}{l}M - P\\ = \left( {3{{{x}}^3} - {x^2}y + 2{{x}}y + 2} \right) - \left( {3{{{x}}^3} - 2{{{x}}^2}y - xy + 3} \right)\\ = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 2 - 3{{{x}}^3} + 2{{{x}}^2}y + xy - 3\\ = {x^2}y + 3{{x}}y - 1\end{array}\)

Câu 21 :

Cho các đa thức:

\(\begin{array}{l}M = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 3\\N = {x^2}y - 2{{x}}y - 2\end{array}\)

Tính M + 2N

  • A
    \(3{{{x}}^3} - 1\)               
  • B
    \(3{{{x}}^3} + {x^2}y - 2{{x}}y + 1\)
  • C
    \(3{{{x}}^3} - {x^2}y + 2{{x}}y - 1\)
  • D
    \(3{{{x}}^3} + {x^2}y - 2{{x}}y - 1\)

Đáp án : D

Phương pháp giải :
Tính M + 2N và nhóm các đơn thức đồng dạng
Lời giải chi tiết :

\(\begin{array}{l}M + 2N\\ = \left( {3{{{x}}^3} - {x^2}y + 2{{x}}y + 3} \right) + 2({x^2}y - 2{{x}}y - 2)\\ = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 3 + 2{{{x}}^2}y - 4{{x}}y - 4\\ = 3{{{x}}^3} + {x^2}y - 2{{x}}y - 1\end{array}\)

Đáp án đúng là : D

Câu 22 :

Xác định ba số tự nhiên liên tiếp biết tích hai số đầu nhỏ hơn tích giữa số đầu và số cuối là \(9\).

  • A
    \(9;10;11\).
  • B
    \(8;9;10\).
  • C
    \(10;11;12\).
  • D
    \(7;8;9\).

Đáp án : A

Phương pháp giải :
Gọi 3 số tự nhiên liên tiếp cần tìm là n, n + 1, n +2 từ đó thiết lập công thức và tìm n. Từ đó tìm được ba số tự nhiên liên tiếp.
Lời giải chi tiết :

Gọi ba số tự nhiên liên tiếp là \(n,{\rm{ }}n + 1,{\rm{ }}n + 2\)  \(\left( {n \in \mathbb{N}} \right)\)

Ta có \(n\left( {n + 2} \right) - n\left( {n + 1} \right) = 9\)

\({n^2} + 2n - {n^2} - n = 9\)

\(n = 9\)

Vậy ba số cần tìm là \(9;10;11\)

Câu 23 :

Giá trị biểu thức \({x^4} - 2022{x^3} + 2022{x^2} - 2022x + 2022\) tại \(x = 2021\)là

  • A
    \(2022\).
  • B
    \(2021\).
  • C
    \(1\).
  • D
    \( - 1\).

Đáp án : C

Phương pháp giải :
x = 2021 nên 2022 = x + 1

Ta biến đổi biểu thức đã cho có x + 1 rồi thay các giá trị.

Lời giải chi tiết :
x = 2021 nên 2022 = x + 1

Ta có \({x^4} - 2022{x^3} + 2022{x^2} - 2022x + 2022\)

\( = {x^4} - \left( {x + 1} \right){x^3} + \left( {x + 1} \right){x^2} - \left( {x + 1} \right)x + \left( {x + 1} \right)\)

\( = {x^4} - {x^4} - {x^3} + {x^3} + {x^2} - {x^2} - x + x + 1 = 1\)

Giá trị biểu thức \({x^4} - 2022{x^3} + 2022{x^2} - 2022x + 2022\) tại \(x = 2021\) là \(1\).

Câu 24 :

Cho m số mà mỗi số bằng 3n – 1 và n số mà mỗi số bằng 9 – 3m. Biết tổng tất cả các số đó bằng 5 lần tổng m + n. Khi đó:

  • A
    \(m = \frac{2}{3}n\)
  • B
    \(m = n\)
  • C
    \(m = 2n\)
  • D
    \(m = \frac{3}{2}n\)

Đáp án : A

Phương pháp giải :
Dựa vào đề bài ta viết đa thức thỏa mãn đề bài và tìm mối liên hệ giữa m và n.
Lời giải chi tiết :

+ Tổng của m số mà mỗi số bằng 3n – 1 là m(3n – 1)

+ Tổng của n số mà mỗi số bằng 9 – 3m là n(9 – 3m)

Tổng tất cả các số trên là m(3n – 1) + n(9 – 3m)

Theo đề bài ta có

m(3n – 1) + n(9 – 3m) = 5(m + n)

⇔ 3mn – m + 9n – 3mn = 5m + 5n

⇔ 6m = 4n ⇔ \(m = \frac{2}{3}n\)

Câu 25 :

Cho B = (m – 1)(m + 6) – (m + 1)(m – 6). Chọn kết luận đúng.

  • A
    B ⁝ 10 với mọi m Є Z          
  • B
    B ⁝ 15 với mọi m Є Z 
  • C
    B ⁝ 9 với mọi m Є Z            
  • D
    B ⁝ 20 với mọi m Є Z 

Đáp án : A

Phương pháp giải :
Ta triển khai đa thức B theo quy tắc đa thức nhân với đa thức.
Lời giải chi tiết :

Ta có B = (m – 1)(m + 6) – (m + 1)(m – 6)

          = m2 + 6m – m – 6 – (m2 – 6m + m – 6)

          = m2 + 5m – 6 – m2 + 6m – m + 6 = 10m

Nhận thấy 10 ⁝ 10 ⇒ 10.m ⁝ 10 nên B ⁝ 10 với mọi giá trị nguyên của m.

Câu 26 :

Cho x2 + y2 = 2, đẳng thức nào sau đây đúng?

  • A
    2(x + 1)(y + 1) = (x + y)(x + y – 2)                    
  • B
    2(x + 1)(y + 1) = (x + y)(x + y + 2)
  • C
    2(x + 1)(y + 1) =  x + y                   
  • D
    (x + 1)(y + 1) = (x + y)(x + y + 2)

Đáp án : B

Phương pháp giải :
Ta áp dụng quy tắc đa thức nhân đa thức để biển đổi 2(x + 1)(y + 1) và sử dụng x2 + y2 = 2 để tìm ra được đẳng thức đúng.
Lời giải chi tiết :

Ta có 2(x + 1)(y + 1) = 2(xy + x + y + 1) = 2xy + 2x + 2y + 2

Thay x2 + y2 = 2 ta được

2xy + 2x + 2y + x2+ y2

= (x2+ xy + 2x) + (y2 + xy + 2y)

= x(x + y + 2) + y(x + y + 2)

= (x + y)(x + y +2)

Từ đó ta có 2(x + 1)(y + 1) = (x + y)(x + y + 2)

Câu 27 :

Gọi x là giá trị thỏa mãn

(3x – 4)(x – 2) = 3x(x – 9) – 3. Khi đó

  • A
    x < 0                 
  • B
    x < -1                
  • C
    x > 2                 
  • D
    x > 0

Đáp án : A

Phương pháp giải :
Áp dụng quy tắc nhân đa thức với đa thức rồi tìm giá trị x.
Lời giải chi tiết :

Ta có:

(3x – 4)(x – 2) = 3x(x – 9) – 3

3x.x+ 3x.(-2) – 4.x – 4.(-2) = 3x.x + 3x.(-9) – 3

3x2 – 6x - 4x + 8 = 3x2 – 27x – 3

17x = -11  

\(x = \frac{{ - 11}}{{17}}\)

Vậy \(x = \frac{{ - 11}}{{17}} < 0\)

Câu 28 :

Kết quả rút gọn biểu thức  \(3x\left( {x - 5y} \right) + \left( {y - 5x} \right)\left( { - 3y} \right) - 3\left( {{x^2} - {y^2}} \right) - 1\) là

  • A
    \(3\).
  • B

    \(0\).

  • C

    \( - 1\). 

  • D

    \(1\).

Đáp án : C

Phương pháp giải :
Áp dụng quy tắc nhân đơn thức với đa thức rối rút gọn biểu thức.
Lời giải chi tiết :

\(3x\left( {x - 5y} \right) + \left( {y - 5x} \right)\left( { - 3y} \right) - 3\left( {{x^2} - {y^2}} \right) - 1 \\= 3{x^2} - 15xy - 3{y^2} + 15xy - 3{x^2} + 3{y^2} - 1 \\= \left(3{x^2}- 3{x^2}\right) - \left(15xy - 15xy\right) - \left(3{y^2}   - 3{y^2}\right) - 1 \\=  - 1\)

Câu 29 :

Giá trị \(x\), thỏa mãn \(3x\left( {12x - 4} \right) - 9x\left( {4x - 3} \right) = 30\) là

  • A
    \(0\).
  • B
    \(3\).
  • C
    \(1\).
  • D
    \(2\).

Đáp án : D

Phương pháp giải :
Áp dụng quy tắc nhân đơn thức với đa thức và quy tắc chuyển vế để tìm giá trị x.
Lời giải chi tiết :

\(3x\left( {12x - 4} \right) - 9x\left( {4x - 3} \right) = 30\)

\(36x^2 -  12x - 36x^2 + 27x = 30\)

\(15x = 30\)

\(x = 2\)

Vậy \(x = 2\)

Câu 30 :

Rút gọn biểu thức \(\left( {3x - 5} \right)\left( {2x + 11} \right) - \left( {2x + 3} \right)\left( {3x + 7} \right)\). Khẳng định nào sau đây là đúng?

  • A
    \(6{x^2} - 15x + 55\).
  • B
    Không phụ thuộc vào giá trị của biến \(x\).
  • C
    \( - 43x - 55\).
  • D
    76.

Đáp án : B

Phương pháp giải :
Rút gọn biểu thức theo quy tắc nhân đa thức với đa thức rồi kết luận.
Lời giải chi tiết :

\(\left( {3x - 5} \right)\left( {2x + 11} \right) - \left( {2x + 3} \right)\left( {3x + 7} \right)\)

\( = \left( {6{x^2} + 23x - 55} \right) - \left( {6{x^2} + 23x + 21} \right)\)

\( = 6{x^2} + 23x - 55 - 6{x^2} - 23x - 21 =  - 76\)

Vậy giá trị biểu thức không phụ thuộc vào giá trị của biến \(x\).

Câu 31 :

Giá trị \(m\) thỏa mãn \(\left( {{x^2} - x + 1} \right)x - \left( {x + 1} \right){x^2} + m - 5 =  - 2{x^2} + x\) là

  • A
    \( - 5\).
  • B
    \(5\).
  • C
    \(4\).
  • D
    \(15\).

Đáp án : B

Phương pháp giải :
Áp dụng quy tắc nhân đơn thức với đa thức và cho các giá trị tương ứng có hệ số bằng nhau.
Lời giải chi tiết :

\(\left( {{x^2} - x + 1} \right)x - \left( {x + 1} \right){x^2} + m - 5 =  - 2{x^2} + x\)

\({x^3} - {x^2} + x - {x^3} - {x^2} + m - 5 =  - 2{x^2} + x\)

\( - 2{x^2} + x + m - 5 =  - 2{x^2} + x\)

Vậy giá trị \(m\)cần tìm là  \(m = 5\).

Câu 32 :

Hệ số của \({x^3}\) và \({x^2}\)trong đa thức \(B = \left( {{x^3} - 3{x^2} + 2x + 1} \right)\left( { - {x^2}} \right) - x\left( {2{x^2} - 3x + 1} \right)\) là

  • A
    \( - 4;2\).
  • B
    \(4; - 2\).
  • C
    \(2;4\).
  • D
    \( - 4; - 2\).

Đáp án : A

Phương pháp giải :
Thực hiện rút gọn đa thức B bằng cách sử dụng quy tắc nhân đơn thức với đa thức.
Lời giải chi tiết :

\(B = \left( {{x^3} - 3{x^2} + 2x + 1} \right)\left( { - {x^2}} \right) - x\left( {2{x^2} - 3x + 1} \right)\)

\( =  - {x^5} + 3{x^4} - 2{x^3} - {x^2} - 2{x^3} + 3{x^2} - x\)

\( =  - {x^5} + 3{x^4} - 4{x^3} + 2{x^2} - x\)

Hệ số của \({x^3}\) và \({x^2}\) trong đa thức \(B\) lần lượt là \( - 4\) và \(2\)

Câu 33 :

Giá trị của biểu thức \({x^2}\left( {x + y} \right) - y\left( {{x^2} - {y^2}} \right)\) tại \(x =  - 1;y = 10\) là:

  • A
    \( - 1001\).
  • B
    \(1001\).
  • C
    \(999\).
  • D
    \( - 999\).

Đáp án : C

Phương pháp giải :
Thực hiện quy tắc nhân đơn thức với đa thức để rút gọn biểu thức. Sau đó thay x = -1; y = 10 vào biểu thức đã rút gọn.
Lời giải chi tiết :
Ta có: \({x^2}\left( {x + y} \right) - y\left( {{x^2} - {y^2}} \right) = {x^3} + {x^2}y - y{x^2} + {y^3} = {x^3} + {y^3}\).

Tại \(x =  - 1;y = 10\) thì giá trị biểu thức là: \({\left( { - 1} \right)^3} + {10^3} = 999\)

Câu 34 :

Thực hiện phép tính nhân \(\left( {x - 1} \right)\left( {x + 3} \right)\) ta được kết quả

  • A
    \({x^2} - 3\).
  • B
    \({x^2} + 3\).
  • C
    \({x^2} + 2x - 3\).
  • D
    \({x^2} - 4x + 3\).

Đáp án : C

Phương pháp giải :
Áp dụng quy tắc nhân đa thức với đa thức
Lời giải chi tiết :
Ta có: \(\left( {x - 1} \right)\left( {x + 3} \right) = x.x + x.3 - 1.x - 1.3 = {x^2} + 3x - x - 3 = {x^2} + 2x - 3\)
Câu 35 :

Giá trị của \(a\), \(b\), \(c\) biết \(\left( {a{x^2} + bx + c} \right)\left( {x + 3} \right) = {x^3} + 2{x^2} - 3x\) là

  • A

    \(a = 1\), \(b = 1\), \(c = 0\).

  • B

    \(a = 2\), \(b = 1\), \(c = 1\).

  • C

    \(a = 1\), \(b =  - 1\), \(c = 0\).

  • D

    \(a =  - 1\), \(b = 2\), \(c = 1\).

Đáp án : C

Phương pháp giải :

Áp dụng quy tắc nhân đa thức với đa thức và áp dụng hai đa thức bằng nhau khi các giá trị tương ứng có hệ số bằng nhau. Từ đó tìm ra a, b.

Lời giải chi tiết :

\(\left( {a{x^2} + bx + c} \right)\left( {x + 3} \right) = {x^3} + 2{x^2} - 3x\)

\(a{x^3} + 3a{x^2} + b{x^2} + 3bx + cx + 3c = {x^3} + 2{x^2} - 3x\)

\(a{x^3} + \left( {3a + b} \right){x^2} + \left( {3b + c} \right)x + 3c = {x^3} + 2{x^2} - 3x\)

Suy ra \(a = 1\); \(3a + b = 2\); \(3b + c =  - 3\); \(3c = 0\).

Suy ra \(a = 1\), \(b =  - 1\), \(c = 0\).

Câu 36 :

Thực hiện phép tính nhân \(x\left( {2{x^2} + 1} \right)\) ta được kết quả:

  • A
    \(3{x^2} + x\).
  • B
    \(3{x^3} + x\).
  • C
    \(2{x^3} + x\).
  • D
    \(2{x^3} + 1\).

Đáp án : C

Phương pháp giải :
Áp dụng quy tắc nhân đơn thức với đa thức.
Lời giải chi tiết :
Ta có: \(x\left( {2{x^2} + 1} \right)\) \( = x.2{x^2} + x.1\) \( = 2{x^3} + x\).
Câu 37 :

Với giá trị tự nhiên nào của \(n\) thì phép chia \(\left( {14{x^8}{y^4} - 9{x^{2n}}{y^6}} \right):\left( { - 2{x^7}{y^n}} \right)\) là phép chia hết?

  • A

    \(\frac{7}{2} \le n \le 4\).

  • B

    \(n = 4\).

  • C

    \(n \ge \frac{7}{2}\).

  • D

    \(n \ge 4\).

Đáp án : B

Phương pháp giải :

Để \(\left( {14{x^8}{y^4} - 9{x^{2n}}{y^6}} \right):\left( { - 2{x^7}{y^n}} \right)\) là phép chia hết thì \(\left\{ \begin{array}{l}n \le 4\\2n \ge 7\end{array} \right.\)

Lời giải chi tiết :

Để \(\left( {14{x^8}{y^4} - 9{x^{2n}}{y^6}} \right):\left( { - 2{x^7}{y^n}} \right)\) là phép chia hết thì \(\left\{ \begin{array}{l}n \le 4\\2n \ge 7\end{array} \right.\)\( \Leftrightarrow \frac{7}{2} \le n \le 4\).

Mà \(n\) là số tự nhiên nên \(n = 4\).

Câu 38 :

Cho \(P = \left( {75{x^5}{y^2} - 45{x^4}{y^3}} \right):\left( {3{x^3}{y^2}} \right) - \left( {\frac{5}{2}{x^2}{y^4} - 2x{y^5}} \right):\left( {\frac{1}{2}x{y^3}} \right)\). Khẳng định nào sai?

  • A

    \(P \ge 0,\,\,\forall x,\,\,y \ne 0\).

  • B

    \(P > 0 \Leftrightarrow 5x - 2y \ne 0\).

  • C

    \(P = 0 \Leftrightarrow 5x = 2y \ne 0\).

  • D

    \(P\) nhận cả giá trị âm và dương.

Đáp án : B

Phương pháp giải :

Thực hiện phép tính chia và rút gọn đa thức P. Từ đó xác định dấu của P.

Lời giải chi tiết :

\(P = \left( {75{x^5}{y^2} - 45{x^4}{y^3}} \right):\left( {3{x^3}{y^2}} \right) - \left( {\frac{5}{2}{x^2}{y^4} - 2x{y^5}} \right):\left( {\frac{1}{2}x{y^3}} \right)\)

\(P = 25{x^2} - 15xy - 5xy + 4{y^2}\)

\(P = 25{x^2} - 20xy + 4{y^2}\)

\(P = {\left( {5x - 2y} \right)^2}\)

\( \Rightarrow \)\(P > 0 \Leftrightarrow 5x - 2y \ne 0\).

Câu 39 :

Một cửa hàng buổi sáng bán được xy bao gạo thì của hàng đó thu được số tiền là \({x^6}{y^5} - {x^5}{y^4}\) nghìn đồng. Tính số tiền mỗi bao gạo của cửa hàng đó đã bán khi x = 2; y = 2.

  • A

    384 nghìn đồng                         

  • B

    284 nghìn đồng

  • C

    120 nghìn đồng                         

  • D

    84 nghìn đồng

Đáp án : A

Phương pháp giải :

Viết công thức số tiên tính mỗi bao gạo và rút gọn. Sau đó thay x = 2; y = 2 vào công thức đã rút gọn.

Lời giải chi tiết :

Số tiền mỗi bao gạo của cửa hàng đã bán theo x , y là:

\(\left( {{x^6}{y^5} - {x^5}{y^4}} \right):xy = {x^5}{y^4} - {x^4}{y^3}\) (nghìn đồng)

Số tiền mỗi bao gạo mà cửa hàng đó đã bán khi x = 2; y =2 là:

\({2^5}{.2^4} - {2^4}{.2^3} = 384\) (nghìn đồng)

Câu 40 :

Tìm đơn thức B biết: \(\left( {B + 2{x^2}{y^3}} \right).\left( { - 3xy} \right) =  - 3{x^2}{y^2} - 6{x^3}{y^4}\)

  • A

    \(B = xy\)                   

  • B

    \(B =  - xy\)                       

  • C

    \(B = x + 1\)                 

  • D

    \(B = {x^2}y\)

Đáp án : A

Phương pháp giải :

Áp dụng: \(\left( {B + A} \right).C = D \Rightarrow B = D:C - A\)

Lời giải chi tiết :

Ta có:

\(\begin{array}{l}\left( {B + 2{x^2}{y^3}} \right).\left( { - 3xy} \right) =  - 3{x^2}{y^2} - 6{x^3}{y^4}\\ \Rightarrow B + 2{x^2}{y^3} = \left( { - 3{x^2}{y^2} - 6{x^3}{y^4}} \right):\left( { - 3xy} \right)\\ \Rightarrow B + 2{x^2}{y^3} = xy + 2{x^2}{y^3}\\ \Rightarrow B = xy + 2{x^2}{y^3} - 2{x^2}{y^3}\\ \Rightarrow B = xy\end{array}\)

Câu 41 :

Chọn kết luận đúng về biểu thức:

\(E = \frac{2}{3}{x^2}{y^3}:\left( {\frac{{ - 1}}{3}xy} \right) + 2x\left( {y - 1} \right)\left( {y + 1} \right)\left( {x \ne 0;y \ne 0;y \ne 1} \right)\)

  • A

    Giá trị của biểu thức không phụ thuộc vào biến x.

  • B

    Giá trị của biểu thức không phụ thuộc vào biến y.

  • C

    Giá trị của biểu thức không phụ thuộc vào biến.

  • D

    Giá trị của biểu thức bằng 0.

Đáp án : B

Phương pháp giải :

Rút gọn biểu thức và đưa ra kết luận

Lời giải chi tiết :

Ta có:

\(\begin{array}{l}E = \frac{2}{3}{x^2}{y^3}:\left( {\frac{{ - 1}}{3}xy} \right) + 2x\left( {y - 1} \right)\left( {y + 1} \right)\\E =  - 2x{y^2} + 2x\left[ {y(y + 1) - 1.\left( {y + 1} \right)} \right]\\E =  - 2x{y^2} + 2x\left( {{y^2} - 1} \right)\\E =  - 2x{y^2} + 2x{y^2} - 2x\\E =  - 2x\end{array}\)

Giá trị của biểu thức không phụ thuộc vào biến y.

Câu 42 :

Giá trị của số tự nhiên thỏa mãn điều kiện gì để phép chia \({x^{n + 3}}{y^6}:{x^9}{y^n}\) là phép chia hết?

  • A

    n < 6

  • B

    n = 5

  • C

    n > 6

  • D

    n = 6

Đáp án : D

Phương pháp giải :

Số mũ của số bị chia phải lớn hơn hoặc bằng số chia sẽ thỏa mãn điều kiện chia hết.

Lời giải chi tiết :

Để phép chia \({x^{n + 3}}{y^6}:{x^9}{y^n}\) là phép chia hết:

\(\left\{ {\begin{array}{*{20}{c}}{9 \le n + 3}\\{n \le 6}\\{n \in \mathbb{N}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{n \ge 6}\\{n \le 6}\\{n \in \mathbb{N}}\end{array}} \right. \Leftrightarrow n = 6\)

Câu 43 :

Giá trị của biểu thức: \(A = \left[ {{{\left( {x - y} \right)}^5} + {{\left( {x - y} \right)}^4} + {{\left( {x - y} \right)}^3}} \right]:\left( {x - y} \right)\) với x= 3; y = 1 là:

  • A

    28

  • B

    16

  • C

    20

  • D

    14

Đáp án : A

Phương pháp giải :

Rút gọn giá trị của biểu thức A và thay các giá trị x, y vào biểu thức đã rút gọn.

Lời giải chi tiết :

Ta có:

\(\begin{array}{l}A = \left[ {{{\left( {x - y} \right)}^5} + {{\left( {x - y} \right)}^4} + {{\left( {x - y} \right)}^3}} \right]:\left( {x - y} \right)\\A = {\left( {x - y} \right)^4} + {\left( {x - y} \right)^3} + {\left( {x - y} \right)^2}\end{array}\)

Với x = 3; y = 1 ta có:

\(A = {\left( {3 - 1} \right)^4} + {\left( {3 - 1} \right)^3} + {\left( {3 - 1} \right)^2} = {2^4} + {2^3} + {2^2} = 28\)

Câu 44 :

Tính giá trị của biểu thức

D = \(\left( {15x{y^2}\; + {{ }}18x{y^3}\; + {{ }}16{y^2}} \right){{ }}:{{ }}6{y^2}\;-{{ }}7{x^4}{y^3}\;:{{ }}{x^4}y\) tại \(x = \frac{2}{3}{;^{}}y = 1\) là:

  • A

    \(\frac{{28}}{3}\) 

  • B

    \(\frac{3}{2}\)

  • C

    \(\frac{2}{3}\)

  • D

    \( - \frac{2}{3}\)

Đáp án : D

Phương pháp giải :

Thực hiện phép tính chia để rút gọn đa thức D. Sau đó thay các giá trị x, y vào đa thức đã rút gọn.

Lời giải chi tiết :

Ta có:

\(\begin{array}{l}D = \left( {15x{y^2} + 18x{y^3} + 16{y^2}} \right):6{y^2} - 7{x^4}{y^3}:{x^4}y\\D = 15x{y^2}:6{y^2} + 18x{y^3}:6{y^2} + 16{y^2}:6{y^2} - 7{x^4}{y^3}:{x^4}y\\D = \frac{5}{2}x + 3xy + \frac{8}{3} - 7{y^2}\end{array}\)

Tại \(x = \frac{2}{3}{;^{}}y = 1\) ta có:

\(D = \frac{5}{2}.\frac{2}{3} + 3.\frac{2}{3}.1 + \frac{8}{3} - {7.1^2} = \frac{5}{3} + 2 + \frac{8}{3} - 7 = \frac{{13}}{3} - 5 =  - \frac{2}{3}\)

Câu 45 :

Biểu thức \(D = \left( {9{x^2}{y^2} - 6{x^2}{y^3}} \right):{( - 3xy)^2} + \left( {6{x^5}y + 2{x^4}} \right):\left( {2{x^4}} \right)\) sau khi rút gọn là một đa thức có bậc bằng

  • A

    1.

  • B

    2.

  • C

    3.

  • D

    4.

Đáp án : B

Phương pháp giải :

Phương pháp: Rút gọn biểu thức \({\rm{D}}\) bằng cách thực hiện phép tính chia và tìm bậc của đa thức sau khi rút gọn.

Lời giải chi tiết :

\(D = \left( {9{x^2}{y^2} - 6{x^2}{y^3}} \right):{\left( { - 3xy} \right)^2} + \left( {6{x^5}y + 2{x^4}} \right):\left( {2{x^4}} \right)\)

\(D = \left( {9{x^2}{y^2} - 6{x^2}{y^3}} \right):\left( {9{x^2}{y^2}} \right) + \left( {6{x^5}y + 2{x^4}} \right):\left( {2{x^4}} \right)\)

\(D = 1 - \frac{2}{3}y + 3xy + 1\)

\(D = 2 - \frac{2}{3}y + 3xy\)

Vậy đa thức sau rút gọn có bậc là \(2\).

Câu 46 :

Tất cả các giá trị của \(x\) để \(\left( {2{x^4} - 3{x^3} + {x^2}} \right):\left( { - {x^2}} \right) + 4{(x - 1)^2} = 0\) là

  • A

    \(x \in \left\{ {1;\frac{3}{2}} \right\}\).

  • B

    \(x \in \left\{ { - 1;\frac{3}{2}} \right\}\).

  • C

    \(x \in \left\{ {1; - \frac{3}{2}} \right\}\).

  • D

    \(x \in \left\{ { - 1; - \frac{3}{2}} \right\}\).

Đáp án : A

Phương pháp giải :

Áp dụng quy tắc chia đa thức cho đơn thức để rút gọn vế trái sau đó tìm giá trị của \(x\).

Lời giải chi tiết :

\(\left( {2{x^4} - 3{x^3} + {x^2}} \right):\left( { - {x^2}} \right) + 4{(x - 1)^2} = 0\)

\(\begin{array}{l} \Leftrightarrow  - 2{x^2} + 3x - 1 + 4 \cdot \left( {{x^2} - 2x + 1} \right) = 0\\ \Leftrightarrow 2{x^2} - 5x + 3 = 0\\ \Leftrightarrow 2{x^2} - 2x - 3x + 3 = 0\\ \Leftrightarrow 2x(x - 1) - 3(x - 1) = 0\\ \Leftrightarrow (2x - 3)(x - 1) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{3}{2}}\\{x = 1}\end{array}} \right.\end{array}\)

Vậy \(x \in \left\{ {1;\frac{3}{2}} \right\}\).

Câu 47 :

Đa thức \(N\) thỏa mãn \( - 15{x^6}{y^5} - 20{x^4}{y^4} - 25{x^5}{y^3} = \left( { - 5{x^3}{y^2}} \right)N\) là

  • A

    \(N =  - 3{x^3}{y^3} + 4x{y^2} + 5{x^2}y\).

  • B

    \(N =  - 3{x^2}{y^3} + 4xy + 5{x^2}y\).

  • C

    \(N = 3{x^3}{y^3} + 4x{y^2} + 5{x^2}y\).

  • D

    \(N = 3{x^3}{y^3} + 4x{y^2} + 5xy\).

Đáp án : C

Phương pháp giải :

Áp dụng: \((A = B.N \Rightarrow \)\({{N}} = {{A}}:{{B}}\))

Lời giải chi tiết :

\(\begin{array}{l} - 15{x^6}{y^5} - 20{x^4}{y^4} - 25{x^5}{y^3} = \left( { - 5{x^3}{y^2}} \right).N\\ \Rightarrow N = \left( { - 15{x^6}{y^5} - 20{x^4}{y^4} - 25{x^5}{y^3}} \right):\left( { - 5{x^3}{y^2}} \right)\\N = 3{x^3}{y^3} + 4x{y^2} + 5{x^2}y.\end{array}\)

Câu 48 :

Giá trị của biểu thức \(P = \left[ {{{(3ab)}^2} - 9{a^2}{b^4}} \right]:\left( {8a{b^2}} \right)\) tại \(a = \frac{2}{3};b = \frac{3}{2}\) là

  • A

    \(\frac{{ - 23}}{{16}}\).

  • B

    \(\frac{{ - 25}}{8}\).

  • C

    \(\frac{{ - 15}}{{16}}\).

  • D

    \(\frac{{ - 21}}{8}\).

Đáp án : C

Phương pháp giải :

Thực hiện phép tính chia và thay giá trị \({\rm{a}},{\rm{b}}\) đã cho vào kết quả của phép chia.

Lời giải chi tiết :

\(P = \left[ {{{(3ab)}^2} - 9{a^2}{b^4}} \right]:\left( {8a{b^2}} \right) \\= \left( {9{a^2}{b^2} - 9{a^2}{b^4}} \right):\left( {8a{b^2}} \right) \\= \frac{9}{8}a - \frac{9}{8}a{b^2}\)

Thay \(a = \frac{2}{3};b = \frac{3}{2}\) vào biểu thức \(P\) ta có: \(P = \frac{9}{8} \cdot \frac{2}{3} - \frac{9}{8} \cdot \frac{2}{3} \cdot {\left( {\frac{3}{2}} \right)^2} = \frac{{ - 15}}{{16}}\)

Câu 49 :

Kết quả phép tính \(\left( {7{x^4} - 3{x^5} + 2{x^2}} \right):\left( {\frac{3}{4}{x^2}} \right)\) là một đa thức có hệ số cao nhất bằng

  • A

    \(\frac{{28}}{3}\).

  • B

    -4.

  • C

    \(\frac{8}{3}\).

  • D

    -3.

Đáp án : B

Phương pháp giải :

Thực hiện phép tính chia và tìm hệ số cao nhất của kết quả.

Lời giải chi tiết :

\(\left( {7{x^4} - 3{x^5} + 2{x^2}} \right):\left( {\frac{3}{4}{x^2}} \right) = \frac{{28}}{3}{x^2} - 4{x^3} + \frac{8}{3}\) là đa thức có hệ số cao nhất là -4 .

Câu 50 :

Đa thức \(7{x^3}{y^2}z - 2{x^4}{y^3}\) chia hết cho đơn thức nào dưới đây?

  • A

    \(3{x^4}\).

  • B

    \( - 3{x^4}\).

  • C

    \( - 2{x^3}y\).

  • D

    \(2x{y^3}\).

Đáp án : C

Phương pháp giải :

Các biến của đa thức phải có các biến của đơn thức.

Lời giải chi tiết :

Đa thức \(7{x^3}{y^2}z - 2{x^4}{y^3}\) chia hết cho đơn thức \( - 2{x^3}y\).

Câu 51 :

Thực hiện phép chia \(\left( {2{x^4}y - 6{x^2}{y^7}} \right):\left( {2{x^2}} \right)\) ta được đa thức \(a{x^2}y + b{y^7}(a,b\) là hằng số). Khi đó \(a + b\) bằng

  • A

    -3.

  • B

    -4.

  • C

    -2.

  • D

    -5.

Đáp án : C

Phương pháp giải :

Thực hiện phép chia và xác định \({\rm{a}},{\rm{b}}\). Từ đó tính \(a + b\).

Lời giải chi tiết :

\(\left( {2{x^4}y - 6{x^2}{y^7}} \right):\left( {2{x^2}} \right) = {x^2}y - 3{y^7}\)

\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b =  - 3}\end{array} \Rightarrow a + b =  - 2} \right.{\rm{. }}\)

Câu 52 :

Kết quả phép chia \(\left( {6{x^4}y + 4{x^3}{y^3} - 2xy} \right):(xy)\) là một đa thức có bậc bằng

  • A

    3.

  • B

    4.

  • C

    7.

  • D

    9.

Đáp án : B

Phương pháp giải :

Thực hiện phép chia rồi tìm bậc của kết quả

Lời giải chi tiết :

\(\left( {6{x^4}y + 4{x^3}{y^3} - 2xy} \right):(xy) = 6{x^3} + 4{x^2}{y^2} - 2\) là đa thức có bậc 4 .

Câu 53 :

Kết quả của phép chia \(\left[ {{{(x - y)}^3} - {{(x - y)}^2} + (x - y)} \right]:(y - x)\) là

  • A

    \({(x - y)^2} - (x - y) + 1\).

  • B

    \( - {(x - y)^2} + (x - y) + 1\).

  • C

    \({(x - y)^2} + (x - y) + 1\).

  • D

    \( - {(x - y)^2} + (x - y) - 1\).

Đáp án : D

Phương pháp giải :

Áp dụng quy tắc đa thức chia cho đơn thức

Lời giải chi tiết :

\(\begin{array}{l}\left[ {{{(x - y)}^3} - {{(x - y)}^2} + (x - y)} \right]:(y - x)\\ = {(x - y)^3}:[ - (x - y)] - {(x - y)^2}:[ - (x - y)] + (x - y):[ - (x - y)]\\ =  - {(x - y)^2} + (x - y) - 1\end{array}\)

Câu 54 :

Kết quả của phép chia \(\left( {3{x^3} + 2{x^2} + x} \right):(3x)\) là một đa thức có hệ số tự do là

  • A

    1.

  • B

    \(\frac{2}{3}\).

  • C

    \(\frac{1}{3}\).

  • D

    0.

Đáp án : C

Phương pháp giải :

Áp dụng quy tắc chia đa thức cho đa thức rồi tìm hệ số tự do.

Lời giải chi tiết :

\(\left( {3{x^3} + 2{x^2} + x} \right):(3x) = {x^2} + \frac{2}{3}x + \frac{1}{3}\) là đa thức có hệ số tự do bằng \(\frac{1}{3}\).

Câu 55 :

Kết quả phép chia \(\left( {2{x^3} + 3{x^4} - 12{x^2}} \right):x\) là

  • A

    \(2{x^2} + 3{x^4} - 12{x^2}\).

  • B

    \(2{x^2} + 3{x^3} - 12{x^2}\).

  • C

    \(2{x^2} + 3{x^4} - 12x\).

  • D

    \(2{x^2} + 3{x^3} - 12x\).

Đáp án : D

Phương pháp giải :

Áp dụng quy tắc chia đa thức cho đơn thức.

Lời giải chi tiết :

\(\left( {2{x^3} + 3{x^4} - 12{x^2}} \right):x = \left( {2{x^3}:x} \right) + \left( {3{x^4}:x} \right) - \left( {12{x^2}:x} \right) = 2{x^2} + 3{x^3} - 12x\)

Bài liên quan
close