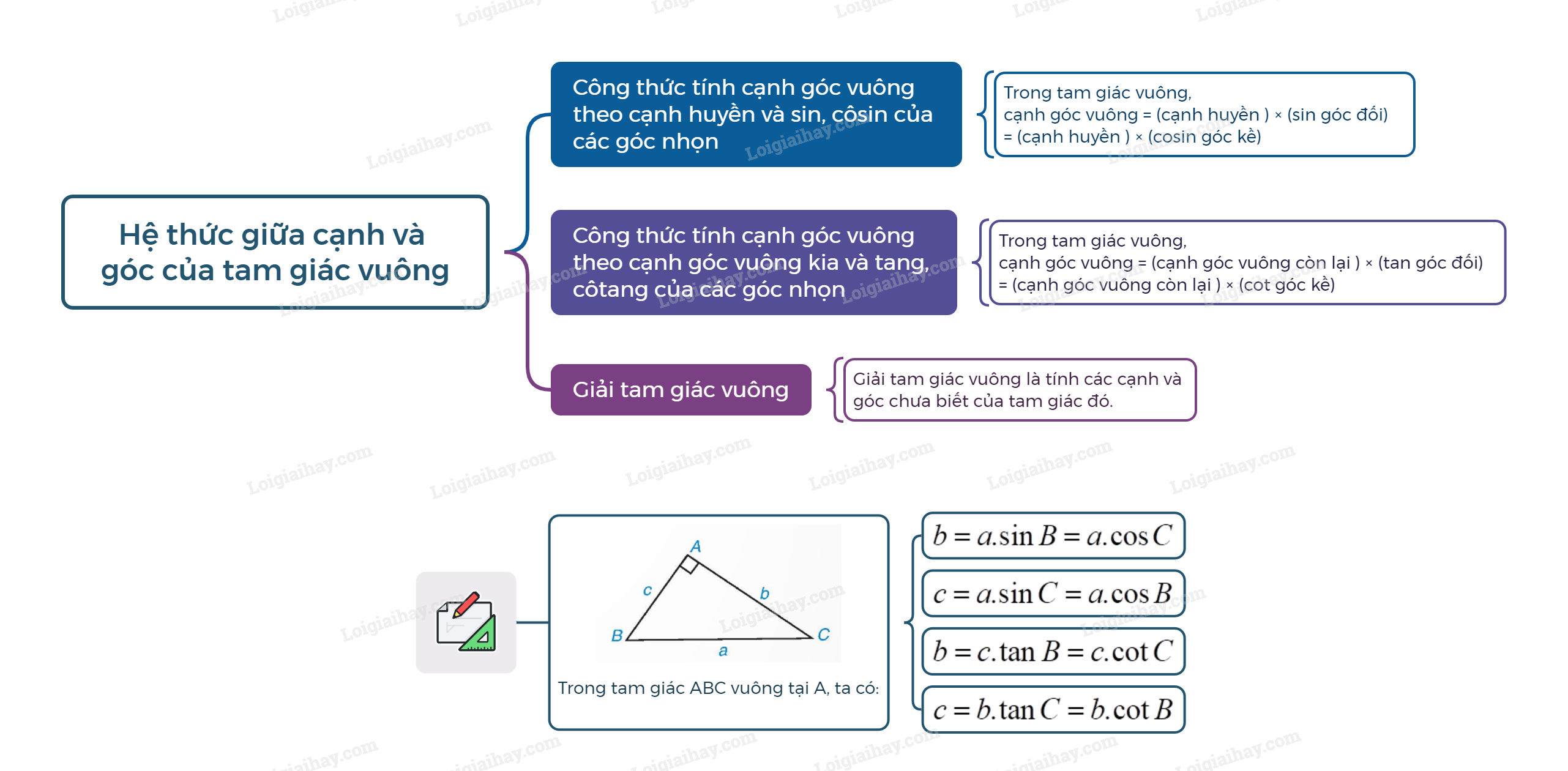
Lý thuyết Hệ thức giữa cạnh và góc của tam giác vuông Toán 9 Chân trời sáng tạo1. Hệ thức giữa cạnh và góc của tam giác vuông Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn Quảng cáo
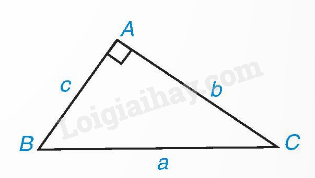
1. Hệ thức giữa cạnh và góc của tam giác vuông Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn
Ví dụ 1:
Trong tam giác ABC vuông tại A, ta có: \(\begin{array}{l}b = a.\sin B = a.\cos C;\\c = a.\sin C = a.\cos B.\end{array}\) Công thức tính cạnh góc vuông theo cạnh góc vuông kia và tang, côtang của các góc nhọn
Ví dụ 2:
Trong tam giác ABC vuông tại A, ta có: \(\begin{array}{l}b = c.\tan B = c.\cot C;\\c = b.\tan C = b.\cot B.\end{array}\) 2. Giải tam giác vuông Giải tam giác vuông là tính các cạnh và góc chưa biết của tam giác đó.
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
