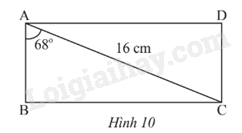
Giải bài tập 1 trang 71 SGK Toán 9 tập 1 - Chân trời sáng tạoTính các cạnh của hình chữ nhật ABCD. Biết AC = 16 cm và (widehat {BAC} = {68^o}) (Hình 10). Quảng cáo
Đề bài Tính các cạnh của hình chữ nhật ABCD. Biết AC = 16 cm và \(\widehat {BAC} = {68^o}\) (Hình 10).
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào định lí: Xét tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông. Lời giải chi tiết Xét tam giác ABC vuông tại B, \(\widehat {BAC} = {68^o}\), ta có: AB = AC .cos\(\widehat {BAC}\) = 16.cos\({68^o} \approx 6 cm\) BC = AC. sin\(\widehat {BAC}\) = 16. sin\({68^o} \approx 14,8 cm\) Vì ABCD là hình chữ nhật nên ta có \(AB = CD \approx 6 cm\) và \(BC = AD \approx 14,8 cm\).
|




















Danh sách bình luận