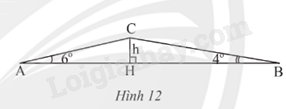
Giải bài tập 4 trang 71 SGK Toán 9 tập 1 - Chân trời sáng tạoLúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762m, (widehat A = {6^o},widehat B = {4^o}). a) Tính chiều cao h của con dốc b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ khi lên dốc là 4 km/h và tốc độ khi xuống dốc là 19 km/h. Quảng cáo
Đề bài Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762m, \(\widehat A = {6^o},\widehat B = {4^o}\). a) Tính chiều cao h của con dốc b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ khi lên dốc là 4 km/h và tốc độ khi xuống dốc là 19 km/h.
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Đặt AH = x sau đó áp dụng hệ thức về cạnh và góc trong tam giác vuông để viết biểu thức chiều cao h theo x. Giải phương trình ta tìm được h. Áp dụng công thức quãng đường = thời gian . vận tốc để rút ra tính thời gian. Lời giải chi tiết a) Đặt AH = x (m) (0 < x < 762) Suy ra BH = 762 – x (m). Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có: h = x. tan \({6^o}\) và h = (762 – x). tan \({4^o}\) Suy ra x. tan \({6^o}\)= (762 – x). tan \({4^o}\) x.( tan \({6^o}\)+ tan \({4^o}\)) =762. tan \({4^o}\) x = \(\frac{{762.\tan {4^o}}}{{\tan {6^o} + \tan {4^o}}}\) Vậy h = \(\frac{{762.\tan {4^o}}}{{\tan {6^o} + \tan {4^o}}}\). tan \({6^o}\)\( \approx \) 32 m. b) Xét tam giác AHC vuông tại H, \(\widehat A = {6^o}\), ta có: \(AC = \frac{h}{{\sin A}} = \frac{{32}}{{\sin {6^o}}} \approx 306m\) = 0,306 km Xét tam giác BHC vuông tại H, \(\widehat B = {4^o}\), ta có: \(CB = \frac{h}{{\sin B}} = \frac{{32}}{{\sin {4^o}}} \approx 459m\) = 0,459 km Thời gian An đi từ nhà tới trường là: \(t = \frac{{AC}}{4} + \frac{{BC}}{{19}} = \frac{{0,306}}{4} + \frac{{0,459}}{{19}} \approx 0,1\) (h) = 6 phút. Vậy An đến trường khoảng 6 giờ 6 phút.
|




















Danh sách bình luận