Trang chủ
Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức

1. Định nghĩa Khái niệm GTLN, GTNN của hàm số

Quảng cáo

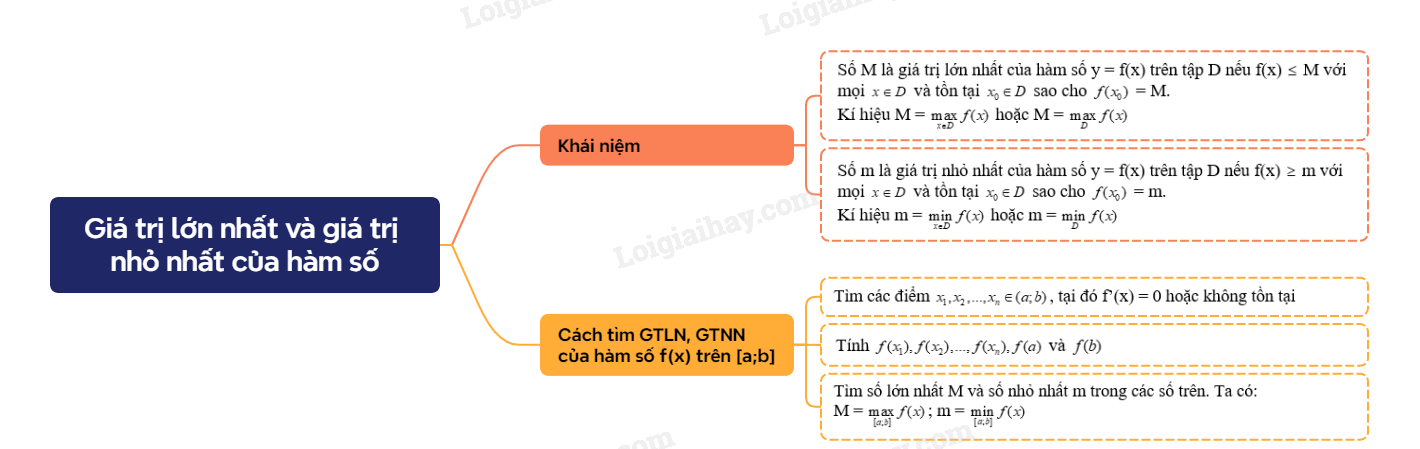
1. Định nghĩa

Khái niệm GTLN, GTNN của hàm số

Cho hàm số y = f(x) xác định trên tập D.

- Số M là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) \( \le \) M với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f({x_0})\) = M.

Kí hiệu M = \(\mathop {\max }\limits_{x \in D} f(x)\) hoặc M = $\underset{D}{\mathop{\max }}\,f(x)$

- Số m là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) \( \ge \) m với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f({x_0})\) = m.

Kí hiệu m = \(\mathop {\min }\limits_{x \in D} f(x)\) hoặc m = \(\mathop {\min }\limits_D f(x)\)

Ví dụ: Tìm GTLN, GTNN của hàm số \(y = f(x) = \sqrt {1 - {x^2}} \)

Tập xác định của hàm số là \(\left[ { - 1;1} \right]\)

Ta có:

\(f(x) = \sqrt {1 - {x^2}} \) \( \ge \) 0; dấu bằng xảy ra khi \(1 - {x^2} = 0\), tức x = -1 hoặc x = 1.

Do đó \(\mathop {\min }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f( - 1) = f(1) = 0\)

\(f(x) = \sqrt {1 - {x^2}} \) \( \le 1\); dấu bằng xảy ra khi \(1 - {x^2} = 1\), tức x = 0.

Do đó \(\mathop {\max }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f(0) = 1\)

2. Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Giả sử y = f(x) là hàm số liên tục trên \(\left[ {a;b} \right]\) và có đạo hàm trên (a;b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn \(\left[ {a;b} \right]\) mà đạo hàm f’(x) = 0.

Các bước tìm GTLN và GTNN của hàm số f(x) trên đoạn \(\left[ {a;b} \right]\):

  1. Tìm các điểm \({x_1},{x_2},...,{x_n} \in (a;b)\), tại đó f’(x) = 0 hoặc không tồn tại
  2. Tính \(f({x_1}),f({x_2}),...,f({x_n}),f(a)\) và \(f(b)\)
  3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:

M = \(\mathop {\max }\limits_{\left[ {a;b} \right]} f(x)\); m = \(\mathop {\min }\limits_{\left[ {a;b} \right]} f(x)\)

Ví dụ: Tìm GTLN và GTNN của hàm số \(y = {x^4} - 4{x^2} + 3\) trên đoạn \(\left[ {0;4} \right]\)

Ta có: \(y' = 4{x^3} - 8x = 4x({x^2} - 2);y' = 0 \Leftrightarrow x = 0\) hoặc \(x = \sqrt 2 \) (vì \(x \in \left[ {0;4} \right]\))

            y(0) = 3; y(4) = 195; y(\(\sqrt 2 \)) = -1

Do đó: \(\mathop {\max }\limits_{\left[ {0;4} \right]} y = y(4) = 195\); \(\mathop {\min }\limits_{\left[ {0;4} \right]} y = y(\sqrt 2 ) =  - 1\)

Quảng cáo
Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
close