Lý thuyết Biểu diễn thập phân của số hữu tỉ Toán 7 Cánh diềuI. Số thập phân hữu hạn và số thập phân vô hạn tuần hoàn Quảng cáo
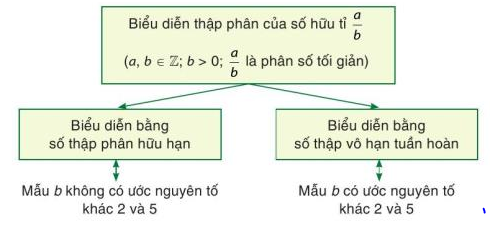
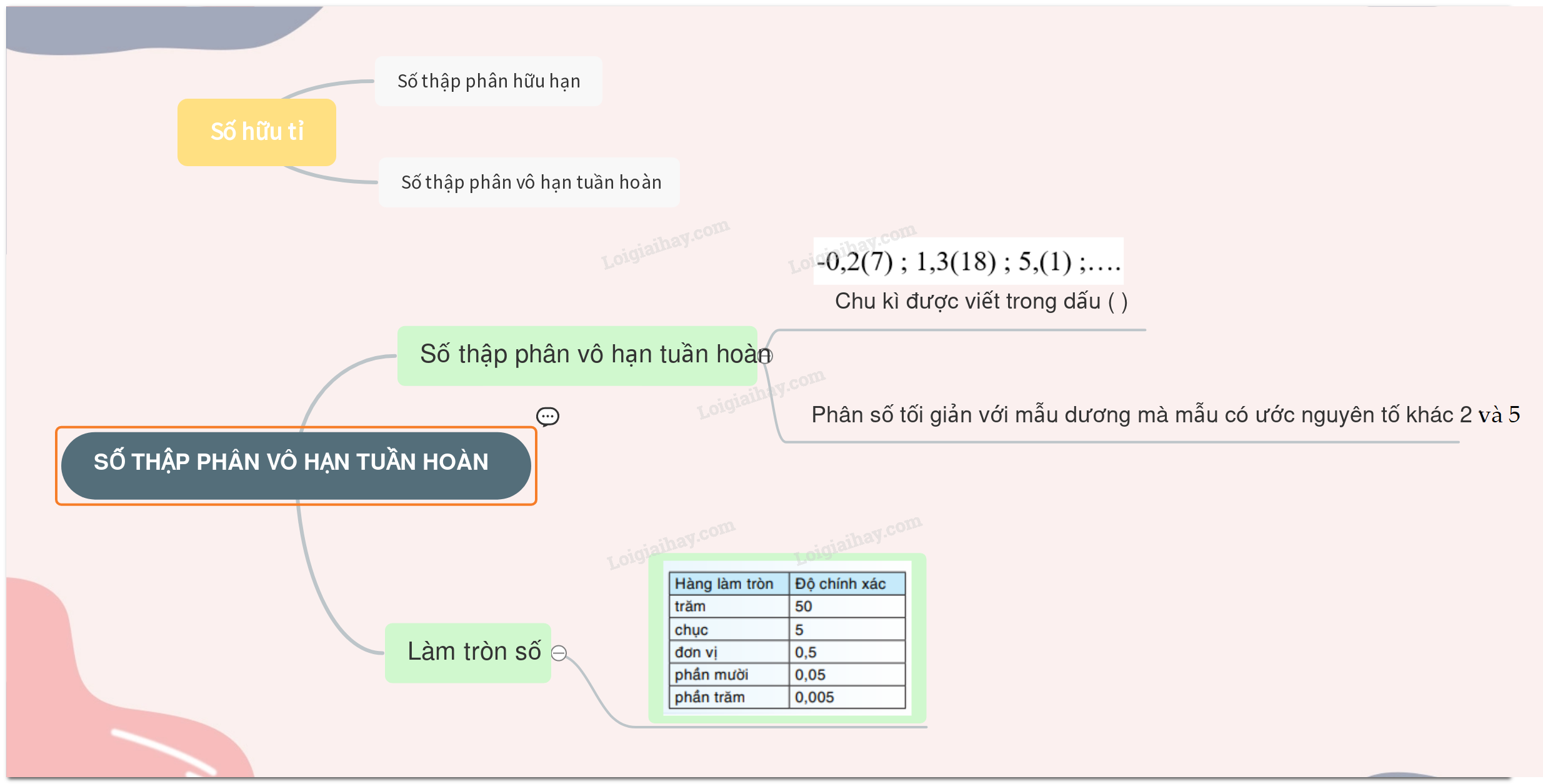
I. Số thập phân hữu hạn và số thập phân vô hạn tuần hoàn Ví dụ: Các số thập phân đã học như -4,3 ; 0,35;… còn được gọi là số thập phân hữu hạn. Các số -0,2(7) ; 1,3(18) ; 5,(1) ;…. là những số thập phân vô hạn tuần hoàn với chu kì lần lượt là 7 ; 18 ; 1. + Mỗi số thập phân vô hạn tuần hoàn biểu diễn 1 số hữu tỉ II. Biểu diễn thập phân của số hữu tỉ + Mọi số hữu tỉ đều viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn. + Nếu phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố nào khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn. Ví dụ: \(\frac{3}{{80}} = \frac{3}{{{2^4}.5}} = \frac{{{{3.5}^3}}}{{{2^4}{{.5.5}^3}}} = \frac{{375}}{{10000}} = 0,0375\) + Nếu phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn. Ví dụ: \(\frac{7}{{30}} = 0,2333.... = 0,2(3)\)
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
